问题:
- 现有的大多数方法 采用 基于编码器的语言模型架构,由于数据标注费用昂贵,只能在有限数量的图像文本对上预训练,导致 图像生成质量和稳定性 欠缺。
现状:
- 大语言模型迅速发展,大语言模型是 decoder-only 结构,可以在大规模的 无标签文本数据 上训练。
有些尝试 利用 LLM 的能力增强 文本生成图像 的 diffusion model 的性能,他们的方法是尝试丰富或改写 用户的文本提示 去引导 diffusion model 的 图像生成过程。
- 主要采用间接方法来弥合两者之间的差距,因此受到低效文本编码器的限制。
方法:
- 利用 大语言模型 文本语义理解的优势,改进 文本生成图像 的 diffusion model。
- 在 denoising U-Net 的 cross-attention 部分 附加一个 简单高效的 网络模块,这个模块可以高效地将 语言模型中的 block-wise representations 整合,以生成输入文本提示的文本编码,以此能够利用 预训练的大语言模型 精确地捕捉 语义信息 和 文字之间的上下文依赖。
- 完全放弃文本编码器,使得 text-to-image diffusion model 摆脱 语言理解性 (language comprehensibility) 的瓶颈,可能显著提升其在可控图像生成中的性能。
一个 Transformer-based 语言模型 可以被改写为 Denoising Diffusion Probabilistic Models 的 denoising 步骤。将 LLM 视为 diffusion model,我们进一步得到 从大语言模型的模块中提取文本编码的理论基础。
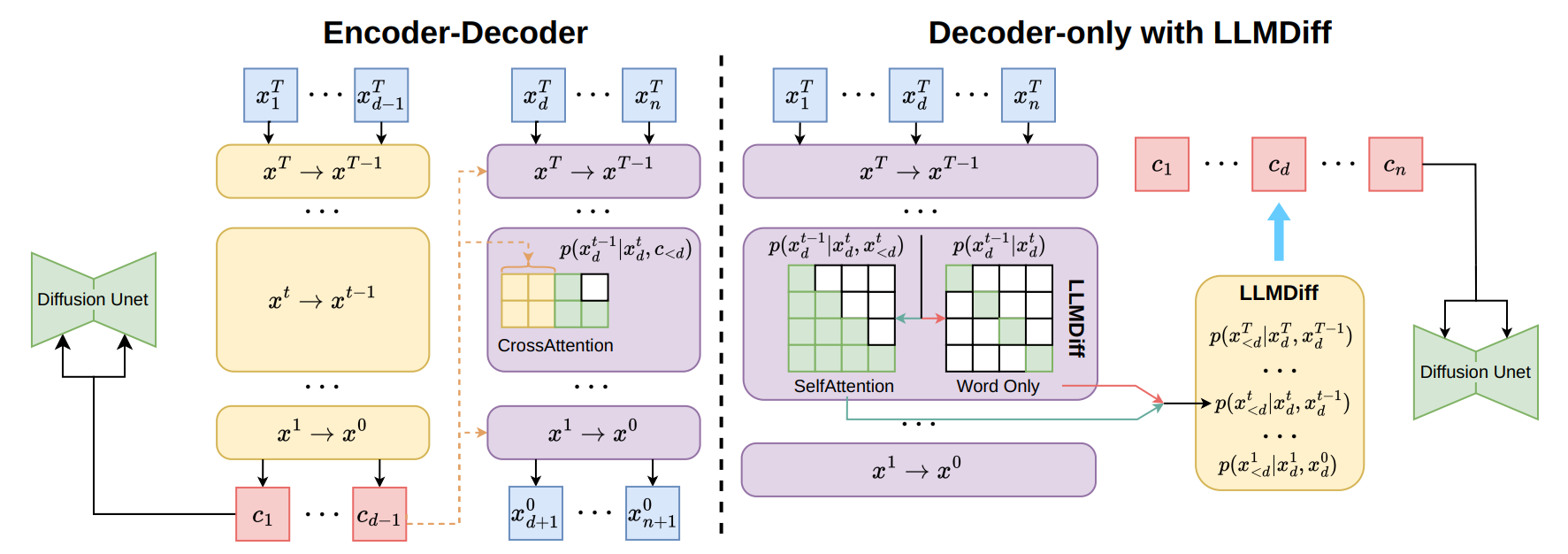
A New Controller for Text-to-Image Generation
Text-to-Image Diffusion Models
- 通常使用编码器对文本输入 $x$ 进行编码,使用 $d-1$ 个 token 作为控制条件 $c_{<d}$
- $c_{<d}$ :通过diffusion model,$p(z_{t-1}|z_t, c_{<d})$ ,生成图像。
diffusion model,使用的 文本编码器 源于预训练模型,如 encoder-only 或 encoder-decoder LLMs。
- encoder-only LLMs 不适用于 文本到图像生成,因为这些模型直接生成 token,无法直接获取文本特征 $c$
LLMs as Diffusion Models
假设 LLM 具有一系列 相同结构的 transformer block。
- 每个输入 token 首先输入 embedding layer
- 第 d 个 token 的 embedding layer 的输出 作为 输入 $x_d^T$ ,然后,它通过 T 个 self-attention 中使用 causal attention masks 的 transformer block,记为 $p_{\theta^t}(x_d^{t-1}|x_d^t, x_{<d}^t)$ ,其中第 $t$ 个块的参数化为 $\theta_t$ 。
- 这个过程类似于 带条件 的 DDPM 的去噪过程。
- 因此,基于 transformer 的 LLM 可以视为 diffusion model。
模型的预测可以表述为:
$$ p_{\theta}(c_d|x_{\leqslant d}) = p(x_d^T)\prod_{t=1}^Tp_{\theta^t}(x_d^{t-1}|x_d^t, x_{<d}^t) $$
Text Encodings from Encoder-Decoder LLMs
- 编码器模型 处理 上下文文本,将其编码为 feature representation,即 文本编码 $c_{<d}$ 。随后,解码器利用这些 text feature 生成单词,满足 $p_{\theta^t}(x_d^{t-1}|x_d^t, c_{<d})$ 。因此,解码器中的每个块都使用相同的条件 $c_{<d}$ 。
- 使用 任一块的输入 $x_d^t$ 和 输出 $x_d^{t-1}$ ,通过贝叶斯定理估计编码 $c_{<d}$ :
$$ p(c_{<d}|x_{d}^{t-1},x_d^t) = \cfrac{p(x_d^{t-1}, x_d^{t} | c_{<d})p(c_{<d})}{p(x_d^{t-1},x_d^t)} $$
Text Encodings from Decoder-only LLMs
- 对于 encoder-only LLM,视为 基于前面的 token 预测下一个 token。
当预测第 d 个单词时,前面的 d-1 个单词共同作为其上下文:
$$ p_{\theta}(x_d|x_{<d}) = p(x_d^T)\prod_{t=1}^Tp_{\theta^t}(x_d^{t-1}|x_d^t, x_{<d}^t) $$
给定 transformer block 的输入 $x_d^t$ 和输出 $x_d^{t-1}$ ,$p(x_{<d}^t|x_d^{t-1}, x_d^t)$ 的估计可以推导如下:
$$ \begin{aligned} p_{\theta^t}(x_{<d}^{t}|x_d^{t-1},x_d^t) &= \cfrac{p(x_d^{t-1},x_d^t|x_{<d}^t)p(x_{<d}^t)}{p(x_d^{t-1},x_d^t)}\\ &= \cfrac{p(x_{d}^{t-1}|x_{\leqslant d}^t)p(x_d^t | x_{<d}^t)p(x_{<d}^t)}{p(x_d^{t-1}|x_d^t)p(x_d^t)}\\ &=\cfrac{p(x_{d}^{t-1}|x_{\leqslant d}^t)p(x_{<d}^t | x_{d}^t)}{p(x_d^{t-1}|x_d^t)}\\ &\propto p(x_d^{t-1}|x_d^t, x_{<d}^t )\ \ \ /\ \ \ p(x_d^{t-1}|x_d^t) \end{aligned} $$
- $p(x_d^{t-1}|x_d^t, x_{<d}^t)$ 是 generative LLM 对 $x_d^t$ 的预测。
- 大多数现有的 LLM 采用 causal mask 作为 attention mask。因此,$p(x_d^{t-1}|x_d^t)$ 可以通过仅将 $x_d^t$ 输入 LLM 来获得,即 $p(x_d^{t-1}|x_d^t) = p(x_d^{t-1}|x_d^t,\emptyset)$ 。
$x_{<d}^t$ 可以视为 下一个 token 预测的条件,发挥与 encoder-decoder LLM 中 $c_{<d}$ 相似的作用。
存在一个 $c_{<d}$ 对于 decoder-only LLM,它是 $x_{<d}$ 的无偏估计。
鉴于 decoder-only LLM 可以视为 diffusion model,我们可以通过 $p_{\theta^t}(x_{<d}^{t}|x_d^{t-1},x_d^t)$ 估计 $p(c_{<d}|x_d^{t-1}, x_d^t)$ 的评分函数,从而获得文本编码 $c_{<d}$ 。
$p(c_{<d}|x_d^{t-1}, x_d^t)$ 的评分函数可以通过以下方式进行逼近:
$$ \nabla_c\log p_{\theta^t}(c_{<d}|x_d^t,x_d^{t-1})\approx g(t)(\nabla_x\log p_{\theta^t}(x_d^{t-1}|x_d^t, x_{<d}^t)-\nabla_x\log p_{\theta^t}(x_d^{t-1}|x_d^t)) $$
$g(t)$ 是一个依赖于时间步长 $t$ 的标量函数。
$p(c_{<d}|x)$ 的评分函数可以近似表示为:
$$ \begin{aligned} \nabla_c\log p_{\theta^t}(c_{<d}|x_d^t,x_d^{t-1}) &\approx g(t)(\log p_{\theta^t}(x_d^{t}| x_{\leqslant d}^{t+1})-\log p_{\theta^t}(x_d^{t-1}| x_{\leqslant d}^t))\\ & -g(t)(\log p_{\theta^t}(x_d^{t}|x_d^{t+1})-\log p_{\theta^t}(x_d^{t-1}|x_d^t)) \end{aligned} $$
Langevin 动力学模拟 一个粒子 在势能场中 运动的过程,同时考虑了 粒子受到的随机扰动。这个随机过程可以用以下微分方程来描述:
$$ dx = \nabla U(x) \text{ d}t + \sqrt{2D}\text{ d}W $$
- $x$ 是粒子的位置
- U(x) 是势能函数,对于 目标分布中的负对数概率密度
- $\text{d}t$ 是时间步长
- $D$ 是扩散系数,控制随机扰动的强度
- $\text{d}W$ 是 布朗运动,表示 随机扰动
Langevin 动力学 通过 势能梯度 ($\nabla U(x)$) 指导粒子向低势能区域移动。每一步都加入一个随机扰动项 ($\sqrt{2D}\text{ d}W$),这允许 粒子跳出局部最小值,增加探索不同区域的可能性。
使用该评分函数进行 Langevin 动力学采样,以获得用于图像生成的最终文本编码:
$$ c_{<d}^{t-1} = c_{<d}^t + \nabla_c \log p_{\theta^t}(c_{<d}|x_d^t, x_d^{t+1}) + \sqrt{2h(t)}\epsilon_t $$
$h(t)$ 是一个可学习的函数,$\epsilon_t\sim \mathcal N(0, I)$
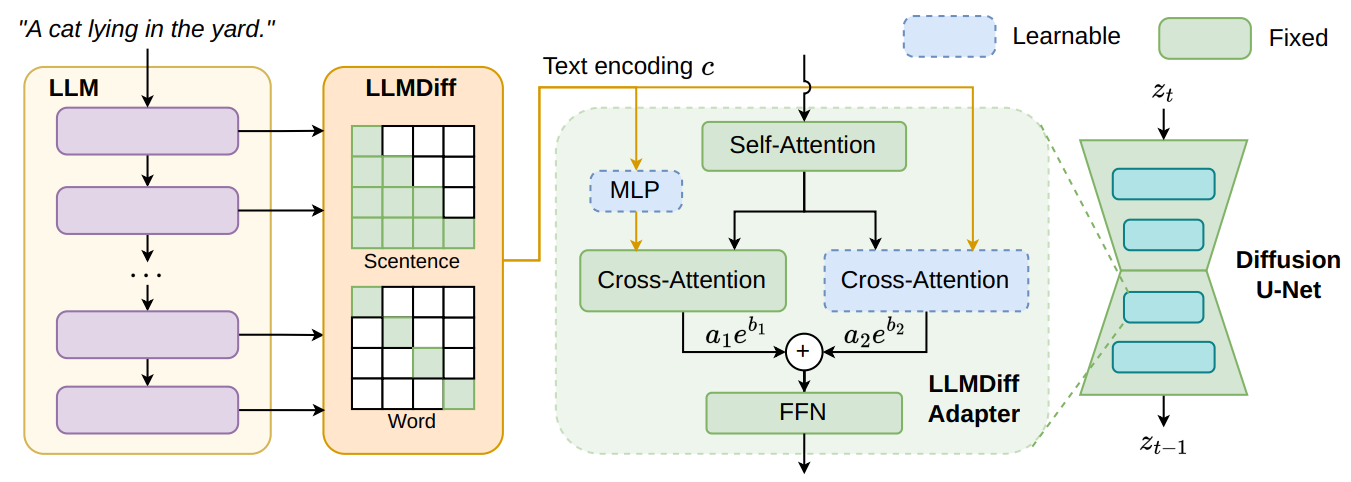
LLMDiff Adapter
Decoder-only LLMs as Diffusion Controller
从 decoder-only LLM 导出适合控制 diffusion image generation models 的文本编码:
$$ c_{<d} = c_{<d}^T + \sum_{T-1}^{t=0}(\nabla_c\log p_{\theta^t}(c_{<d}|x_d^t, x_d^{t+1})+ \sqrt{2h(t)}\epsilon_t) $$
现在利用现有的 transformer block 的 残差结构,可以利用 transformer block 得到 预测分数的模型:
- $S_{\theta^t}(x_d^{t-1}, x_{\leqslant d}^t) \approx \nabla_x\log p(x_d^{t-1} | x_d^t, x_{<d}^t) $
- $S_{\theta^t}(x_d^{t-1}, x_d^t)\approx \nabla_x \log p(x_d^{t-1}| x_d^t) $
LLMDiff Adapter: Bridging Decoder-Only LLMs and Pre-trained Diffusion Models
- 保持原始的 cross-attention module 完好无损,并通过 线性层 将其与来自 LLMs 的编码对齐。
- 引入一个额外的 cross-attention module,以学习如何更好地基于来自 LLMs 的文本编码生成图像。
通过一组可学习的权重因子:$a_1$、$a_2$、$b_1$、$b_2$ ,这两个模块的输出相结合,整体的计算:
$$ f = attn(\hat\tau_q(q), \hat\tau_k(\phi(\mathbf{c})),\hat\tau_v(\phi(\mathbf c))) a_1e^{b_1} + attn(\tau_q(q),\tau_k(\mathbf c),\tau_v(\mathbf c))a_2 e^{b_2} $$
- $\hat\tau$ 是原始 cross-attention module 的线性层,$\tau$ 是附加 cross-attention module 的线性层
- $\phi$ 是 使 LLMs 和 原始的 cross-attention module 对齐的 线性层
LLMDiff Adapter 使用 均方误差 (MSE) 损失函数对 diffusion model 进行训练:
$$ \mathcal L = \| \epsilon_\theta(z_t, \mathbf c)-\epsilon \|^2 $$
$\epsilon_\theta$ 是 diffusion U-Net, $z_t$ 是 时间步 $t$ 的 latent feature map,$\epsilon\sim \mathcal N(0, I)$