Generative Adversarial Network GAN
学习:李宏毅:GAN
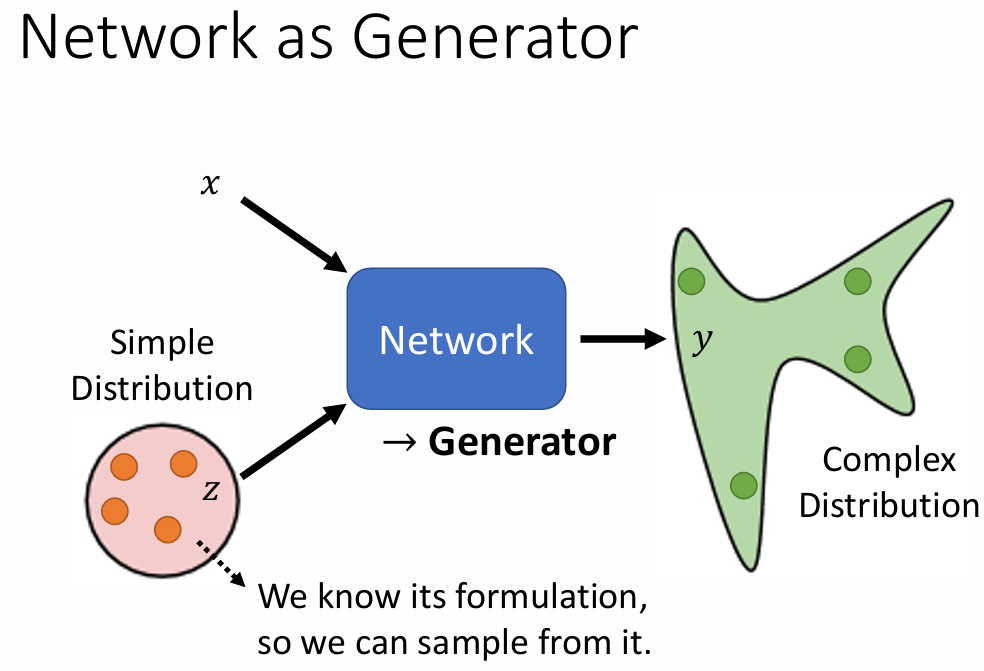
GAN的输入包含一个随机变量 z,该变量从一个简单的分布(通常是正态分布)中采样。随机变量 z 的引入使得生成器具有更强的创造性,从而能够生成多样化的输出。
Unconditional generation
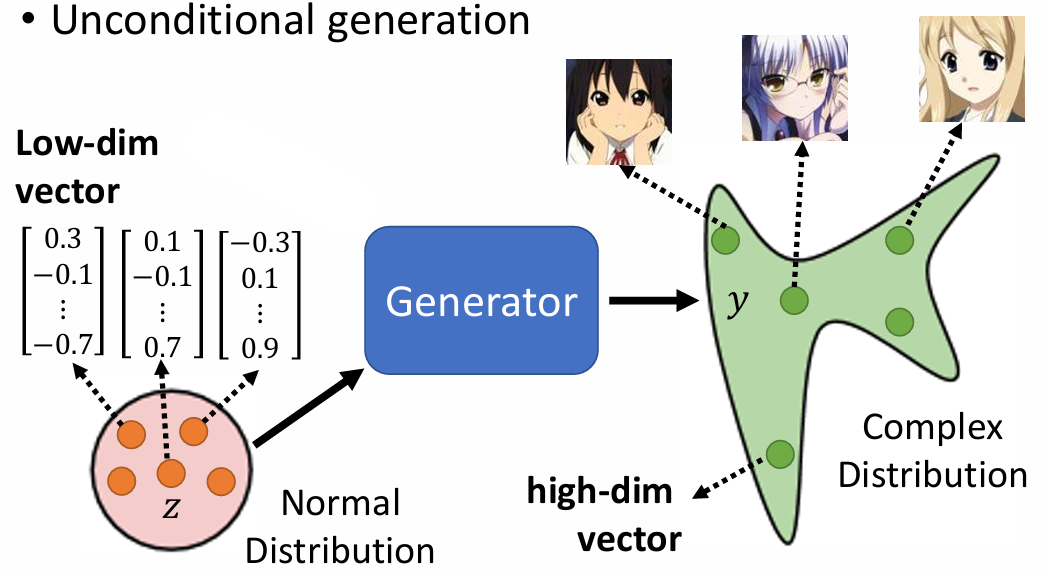
- 输入:一个低维向量 z,来自正态分布。
- 输出:一个高维向量 y,通常表示为一张图像,具有复杂的分布。
输入不同的 z 将导致输出的 y 不相同。
Dicriminator 判别器
- 是一个 neural network
- 输入:一张图像
- 输出:一个数值标量,数值越大,代表图像越真实,越小代表图像越假。
Generator 和 Discriminator 是相互学习一起进化的。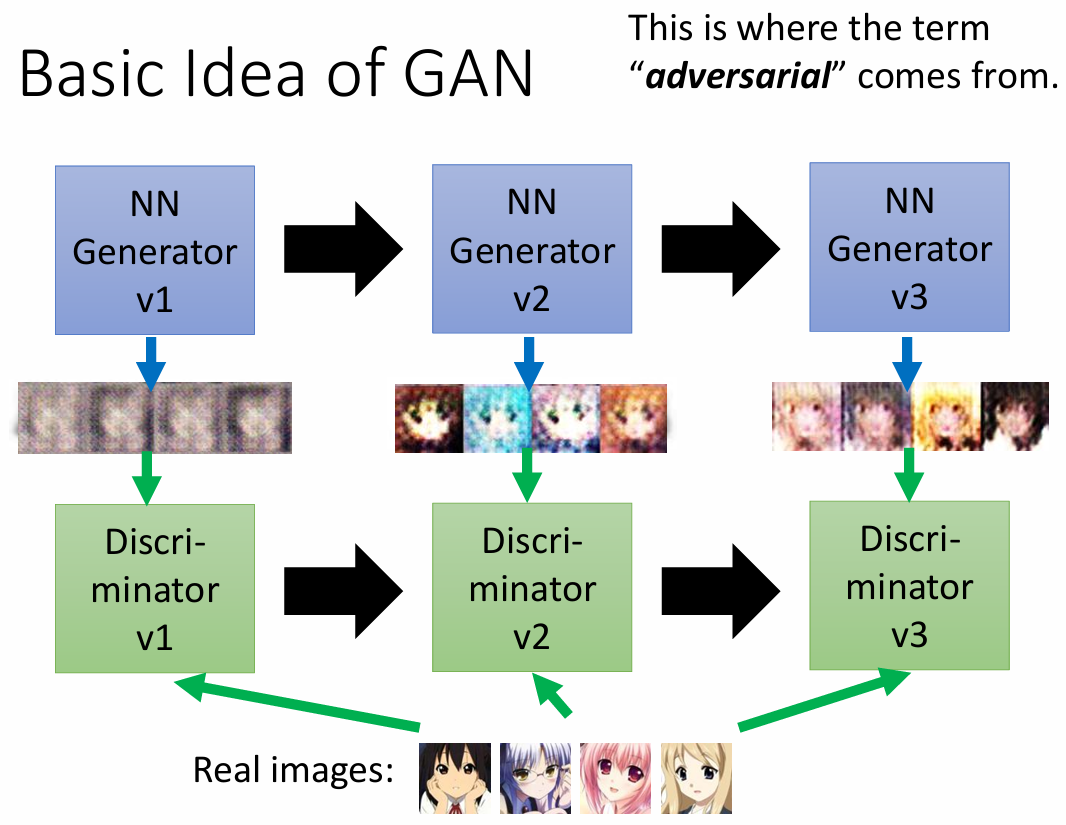
Algorithm
generator 和 discriminator 是两个网络,首先需要初始化 generator 和 discriminator 两个网络,然后在每个训练步:
Step1: 固定 generator G,更新 discriminator D。
从正态分布中采样一些向量,作为 Generator 的输入,得到输出图像
从真实数据集中采样一些真实图像。
然后使用 Discrimintor 对其进行“分类”
- Step2: 固定 discriminator D, 更新 generator G
- generator 尝试 去“欺骗” discriminator,希望生成图像让 Discriminator的输出越大越好。
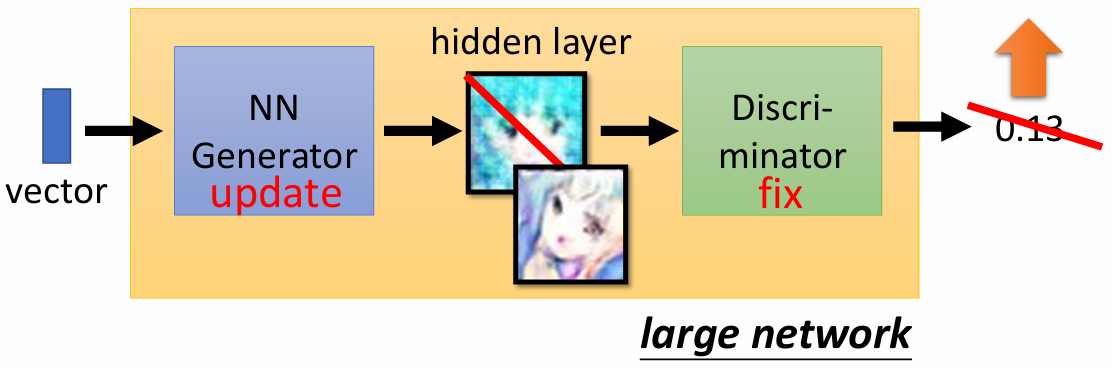
重复进行这两个步骤,直到达到预期效果。
GAN的理论基础
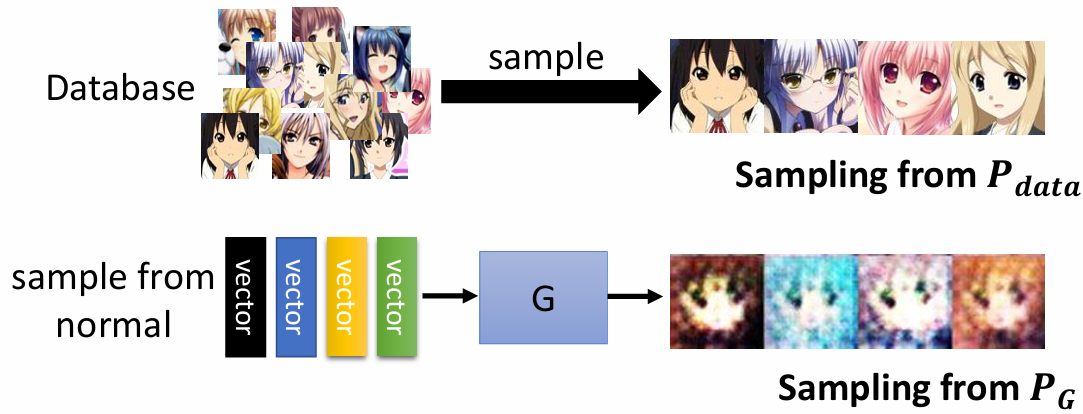
Generator
从 Normal Distribution 采样,作为 Generator 的输入,生成复杂的 Distribution $P_G$ 。
数据集的分布为 $P_{data}$ ,我们希望 $P_G$ 越接近 $P_{data}$ 越好。
$$ G^* = \arg \min_G Div(P_G, P_{data}) $$
$Div(P_G, P_{data})$ 代表 $P_G$ 和 $P_{data}$ 表示两种分布之间的差异 divergence。
如何计算 divergence ?
虽然我们不知道 $P_G$ 和 $P_{data}$ 的分布,但是我们可以采样它们。
Discriminator
判别器的目标是区分真实图像和生成图像,可以看作一个优化问题:
- 训练:$D^* = \arg \max_D V(D, G)$
- D 的目标函数:$V(G, D) = E_{y\sim P_{data}}[\log D(y)] + E_{y\sim P_G}[\log (1-D(y))]$
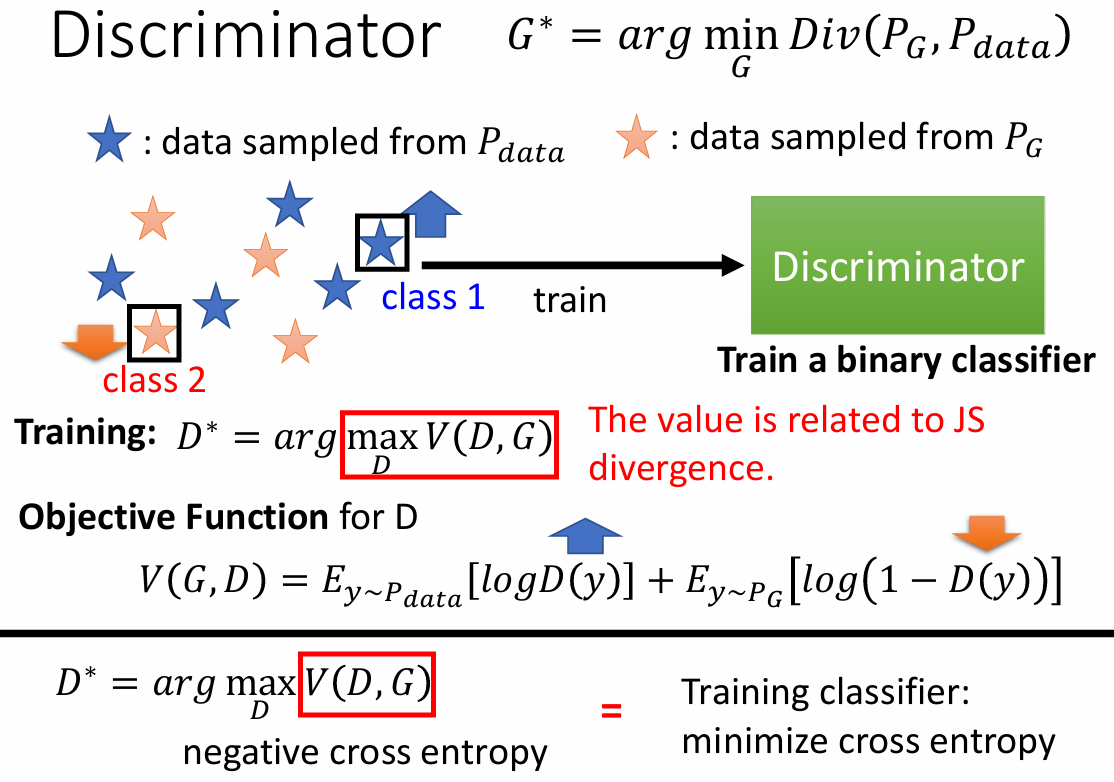
$\max_DV(D,G)$ 和 divergence 有关:当 generator 生成的图像和 真实图像很接近的时候(small divergence),discriminator 很难去辨别,导致 small $\max_DV(D,G)$ 。

WGAN
GAN的问题:
- 大多数情况,$P_G$ 和 $P_{data}$ 不重合
- 数据的属性:$P_{data}$ 和 $P_G$ 都是高维空间的低维 manifold。
采样:即使 $P_{data}$ 和 $P_G$ 有重合,如果没有足够的采样,会很容易设置使得真实图像和生成图像样本之间的分界线(即使得两方样本没有任何重叠的空间)
对于 JS divergence:JS divergence 总是 log2 如果两个分布没有重叠部分。
WGAN提出了Wasserstein距离作为改进方案:
Wasserstein distance:
假设有两个分布 P 和 Q。
设想有两个分布 P 和 Q,通过最小化从 P 推送到 Q 的平均距离来作为分布之间的差异。
$$ \max_{D\in 1-Lipschitz}\{E_{y\sim P_{data}}[D(x)] - P_{y\sim P_G}[D(y)]\} $$
D 要足够平滑,如果是离散的,就容易造成 D(y) 变为无穷。

