1 输入
Self-Attention 的输入一个向量序列,可以是原始输入或者某个隐藏层的输出。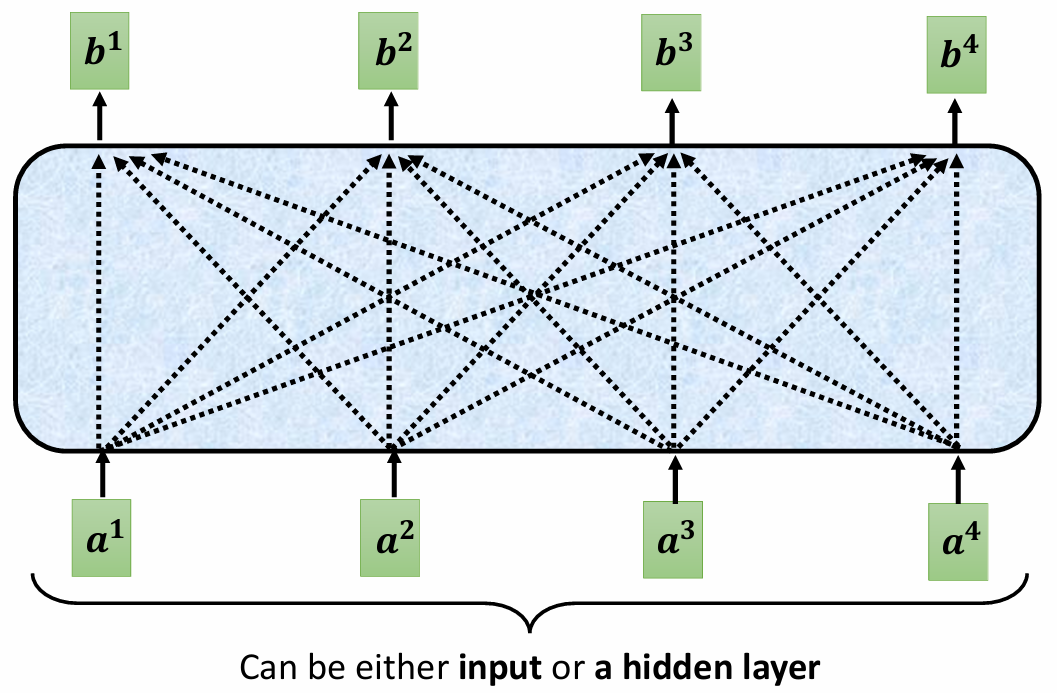
2 输出向量的产生
对于输入向量(例如 $a^1$),需要计算其他向量与 $a^1$ 的关联度。
关联度的计算通常通过 点乘 实现: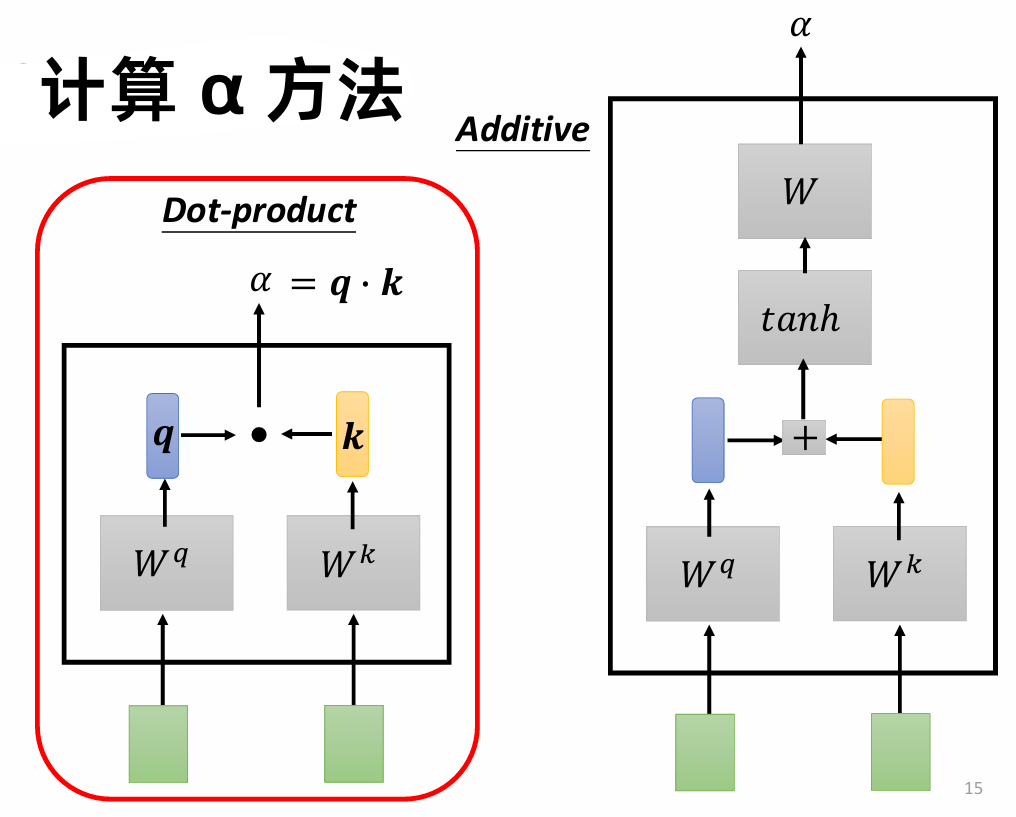
对于给定的输入向量 $a^1$ ,需要先计算 $q^1$ 值:$a^1 = W^qa^1$,其他向量 $a^i$ 计算 $k^i$ 值:$k^i = W^ka^i$,之后和 $q^1$ 点乘,得到 $\alpha_{1,i}$,再进行 soft-max:$\alpha_{1,i}' = \exp(\alpha_{1,i})/\sum_j \exp(\alpha_{1,j})$,作为最终的 attention score:
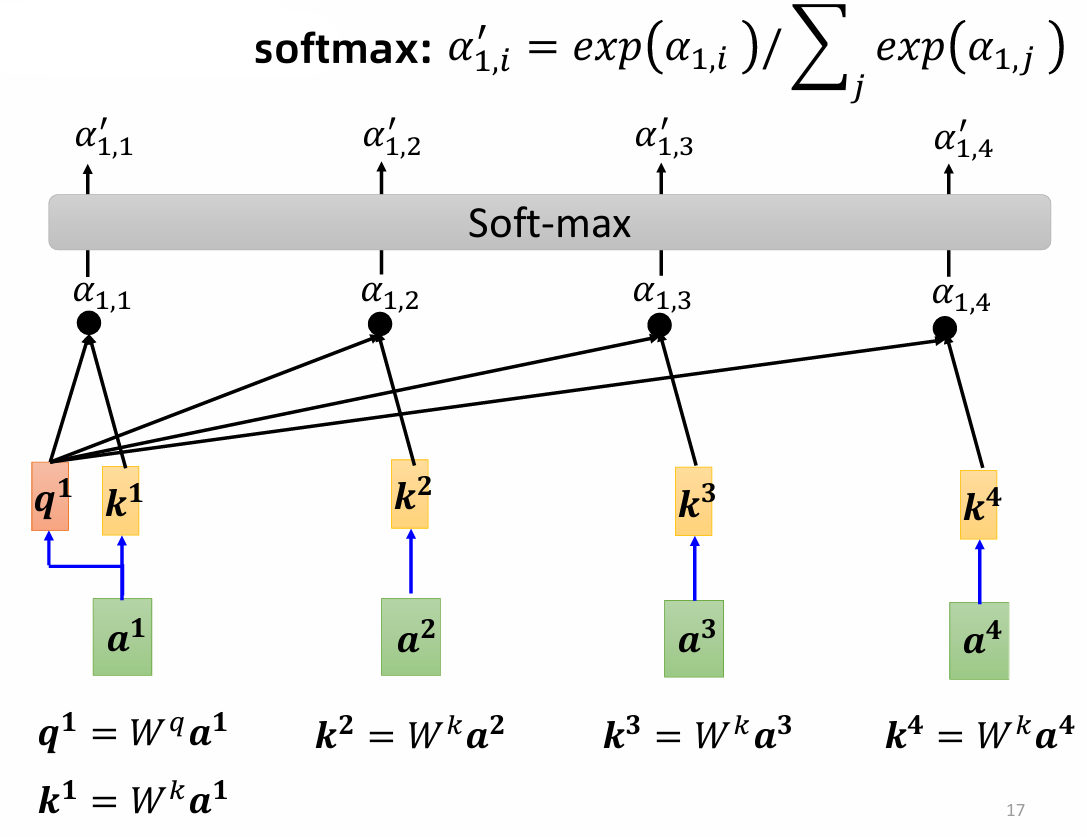
根据 attention score,和每个输入的 value 值相乘(加权求和)得到最终的输出向量:$b^1 = \sum_i \alpha_{1,i}'v^i$
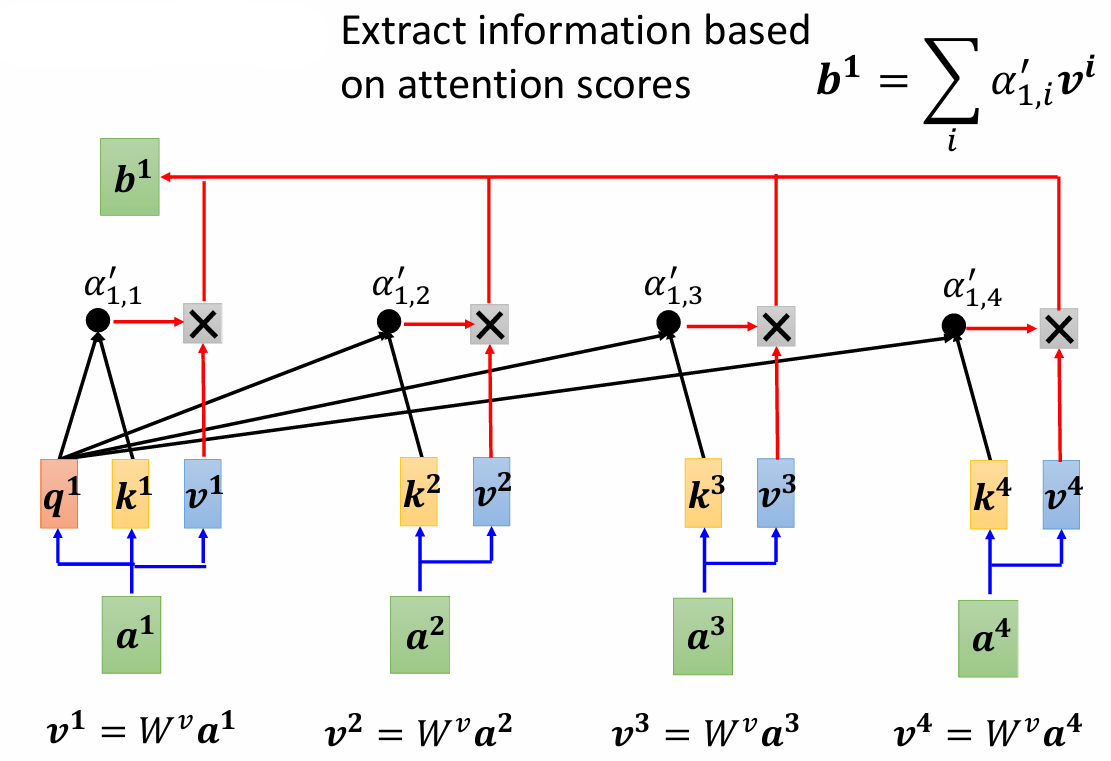
这个输出包含了输入序列中各个元素的信息,经过加权后反映了与查询相关的重要性。
计算 $b^2$,同上:
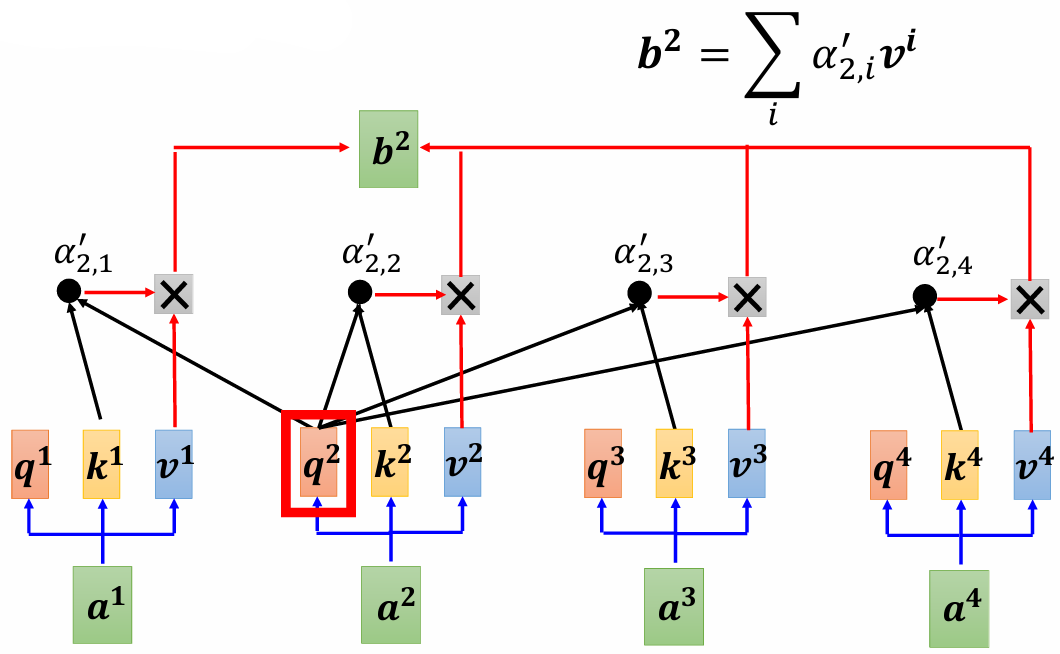
3 矩阵乘法角度理解
从矩阵乘法的角度来看: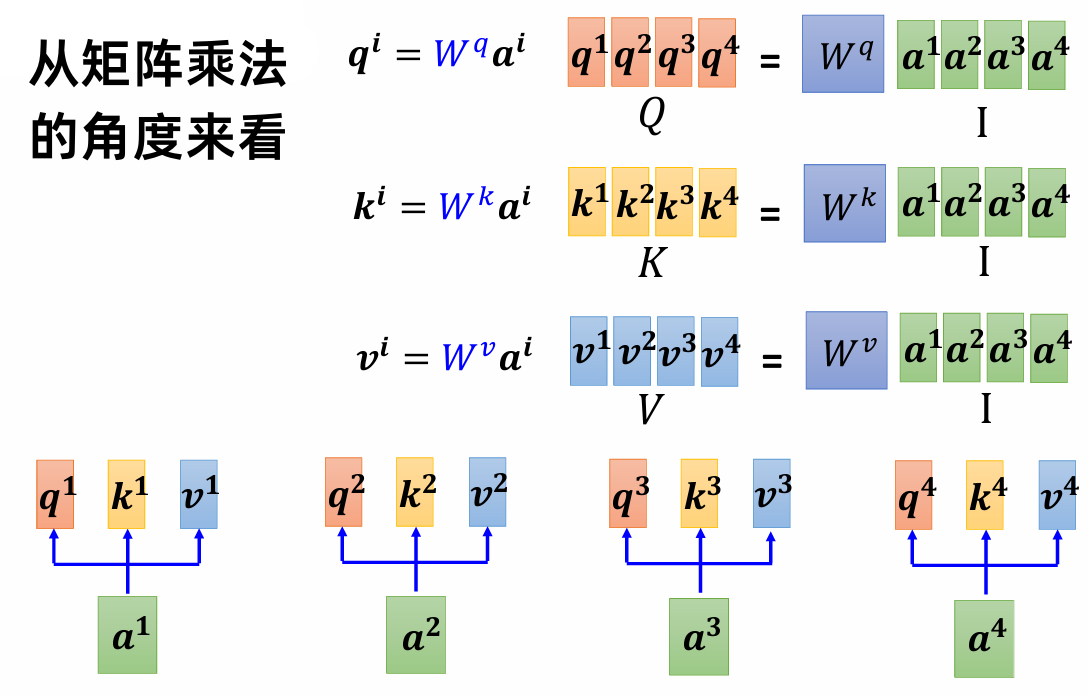
$W^q$,$W^k$,$W^v$ 是需要被学习出来的,矩阵 $I$ 的列向量是 self-attention 的输入向量。
q: query, k: key, v: value
$$ Q =W^q I,K=W^kI,V=W^vI $$
计算单个输入向量与其他向量的关联系数 $\alpha$ 过程看成矩阵向量乘法运算: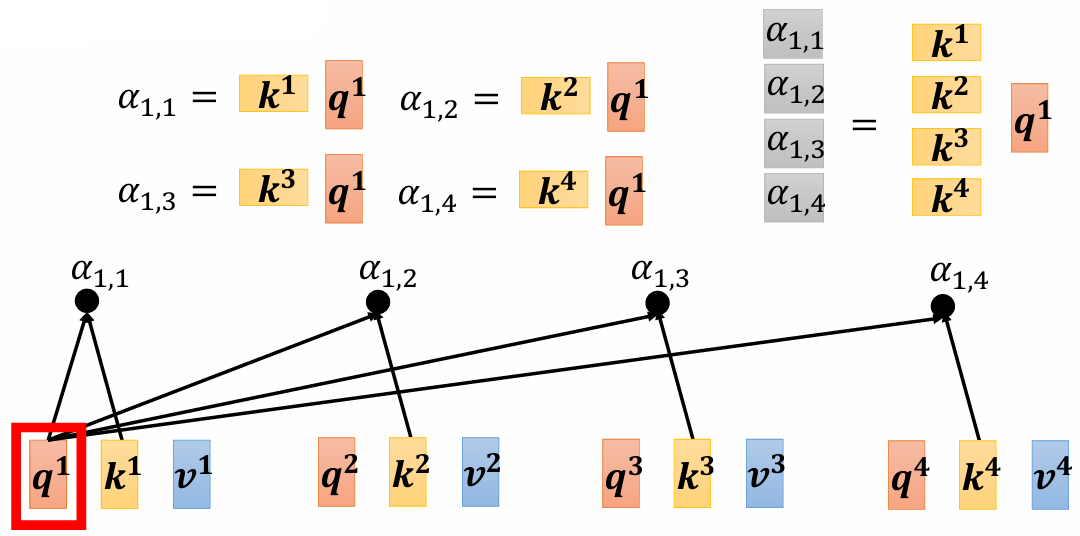

计算 $b$ :
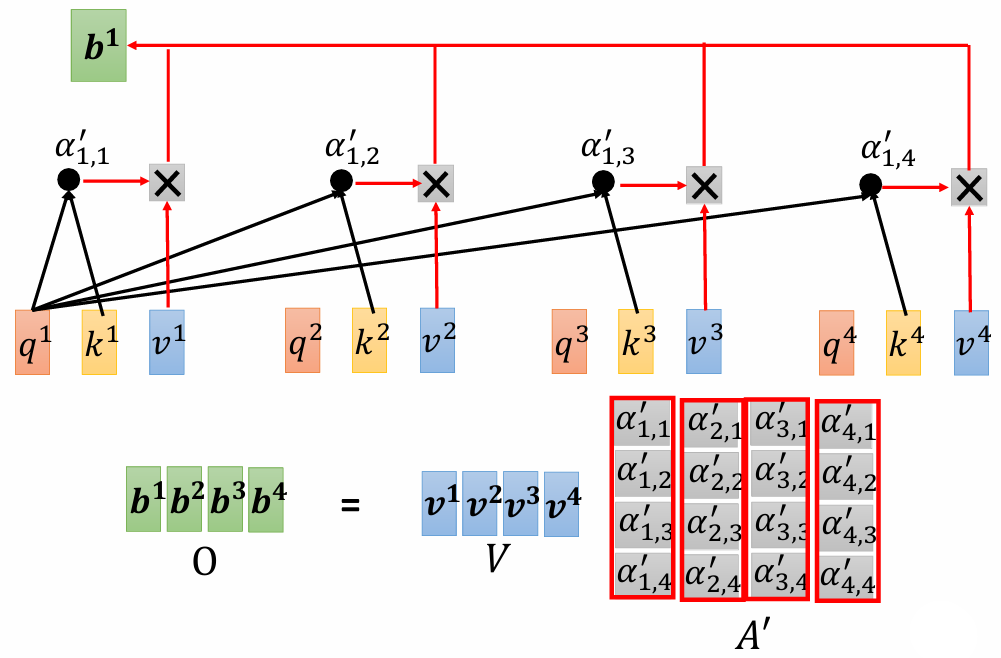
矩阵 $O$ 就是 self-attention 的输出。
self-attention内部运算总结:
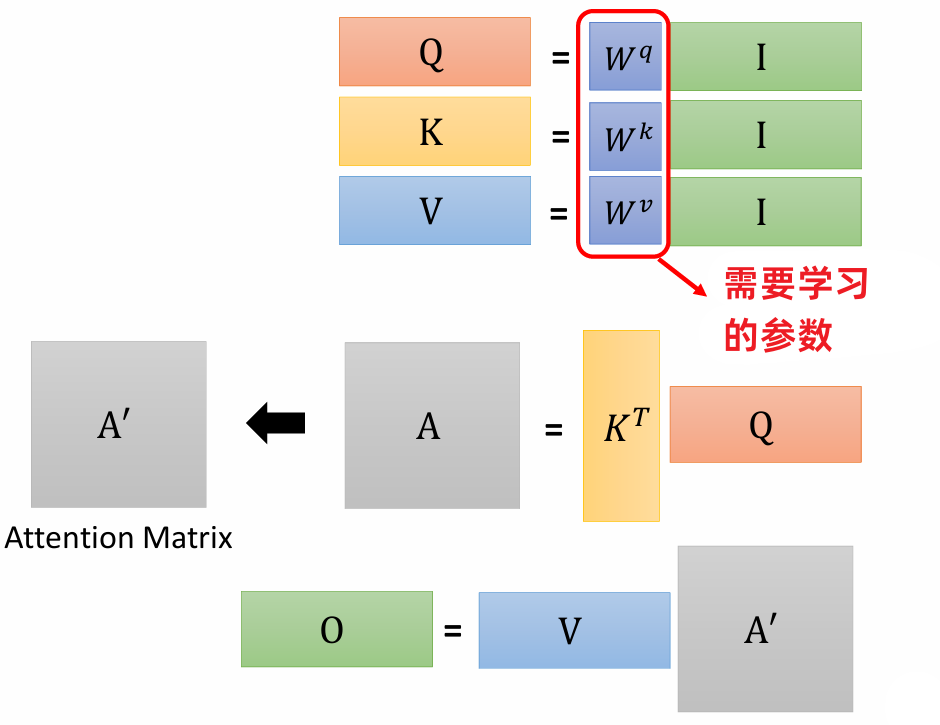
4 Multi-head self-attention
有时候我们需要多个 $q$ 来应付不同的任务场景,产生不同类型的相关性:
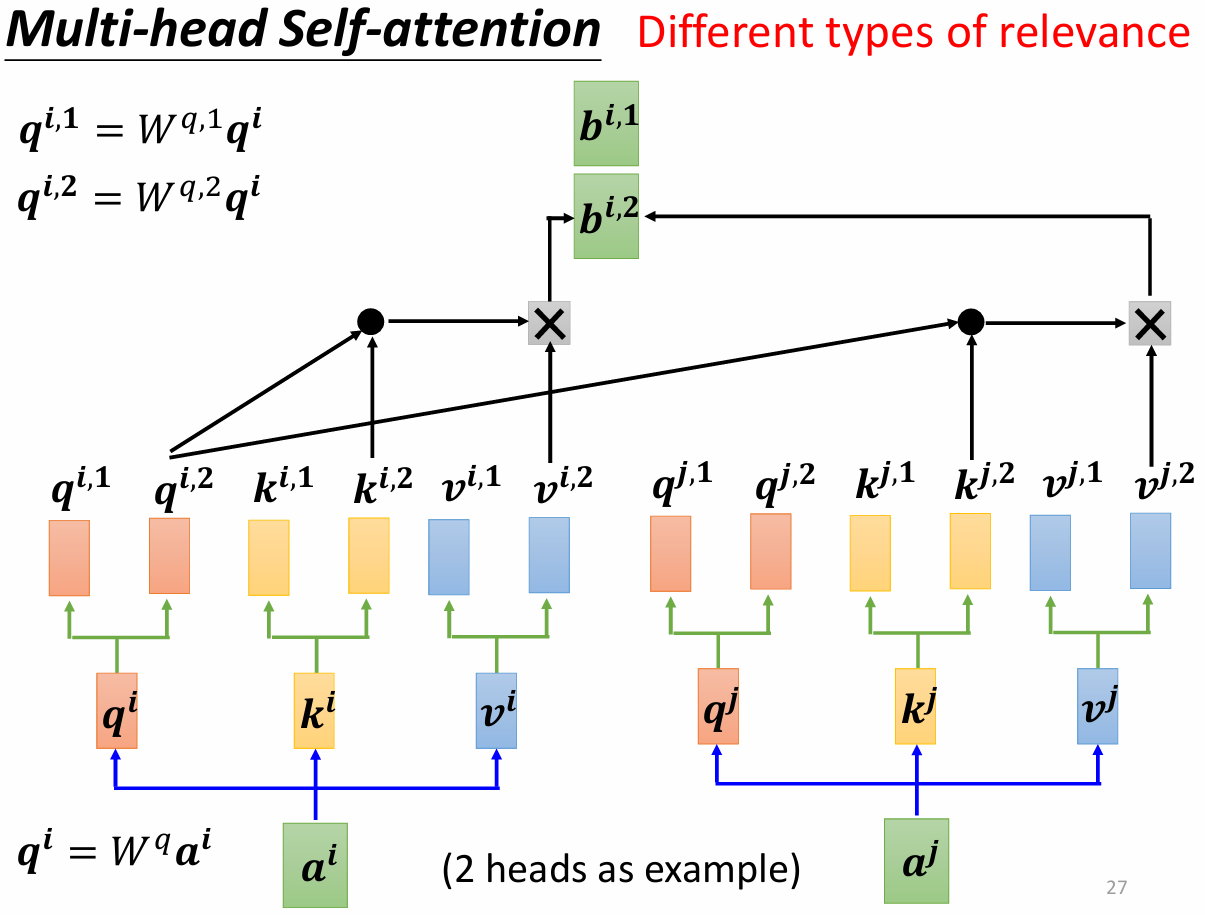
最终的 $b$ 是不同 $b^i$ 的加权和: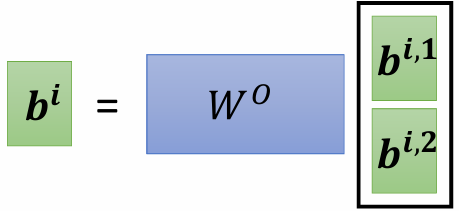
5 位置编码 positional encoding
self-attention 里面没有位置信息,所以可以为每个位置设置唯一的位置向量 $e^i$ ,$e^i$ 加上 $a^i$ 作为输入。位置向量的设置:
- 手工设置 (Hand-Crafted):预定义的位置编码。
- 从数据中学习 (Learned from Data):通过训练数据自动学习的位置编码。
6 self-attention vs CNN / RNN
- CNN:self-attention that can only attend in a receptive field (简化版的 self-attention)
- self-attention: CNN with learnable receptive field
资料较少时,CNN 能获得较好的结果,在资料很多的时候,self-attention 能取得更好的结果。
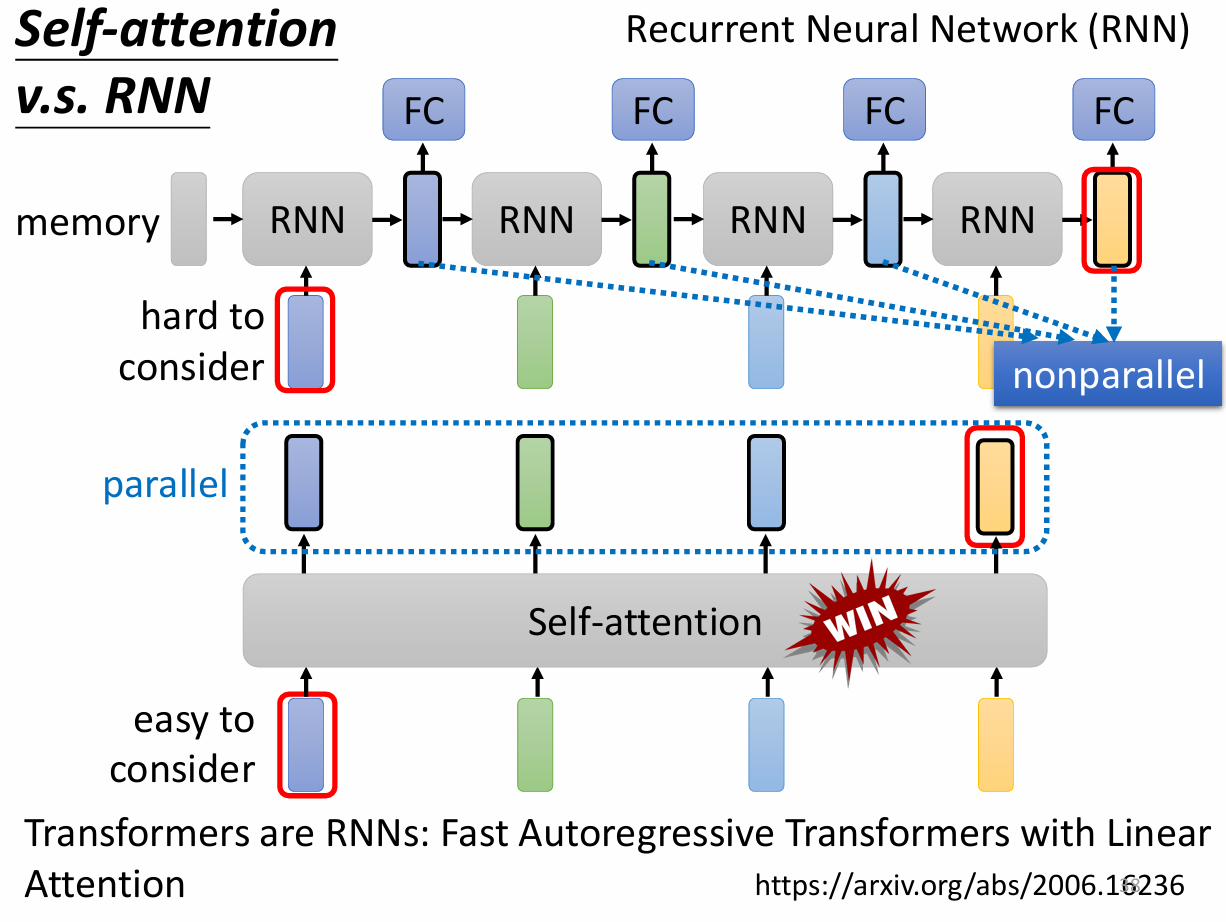
self-attention vs RNN