Diffusion Model

生成式人工智能 · 2024-10-20
Diffusion Model

Diffusion Model 是如何制作的？

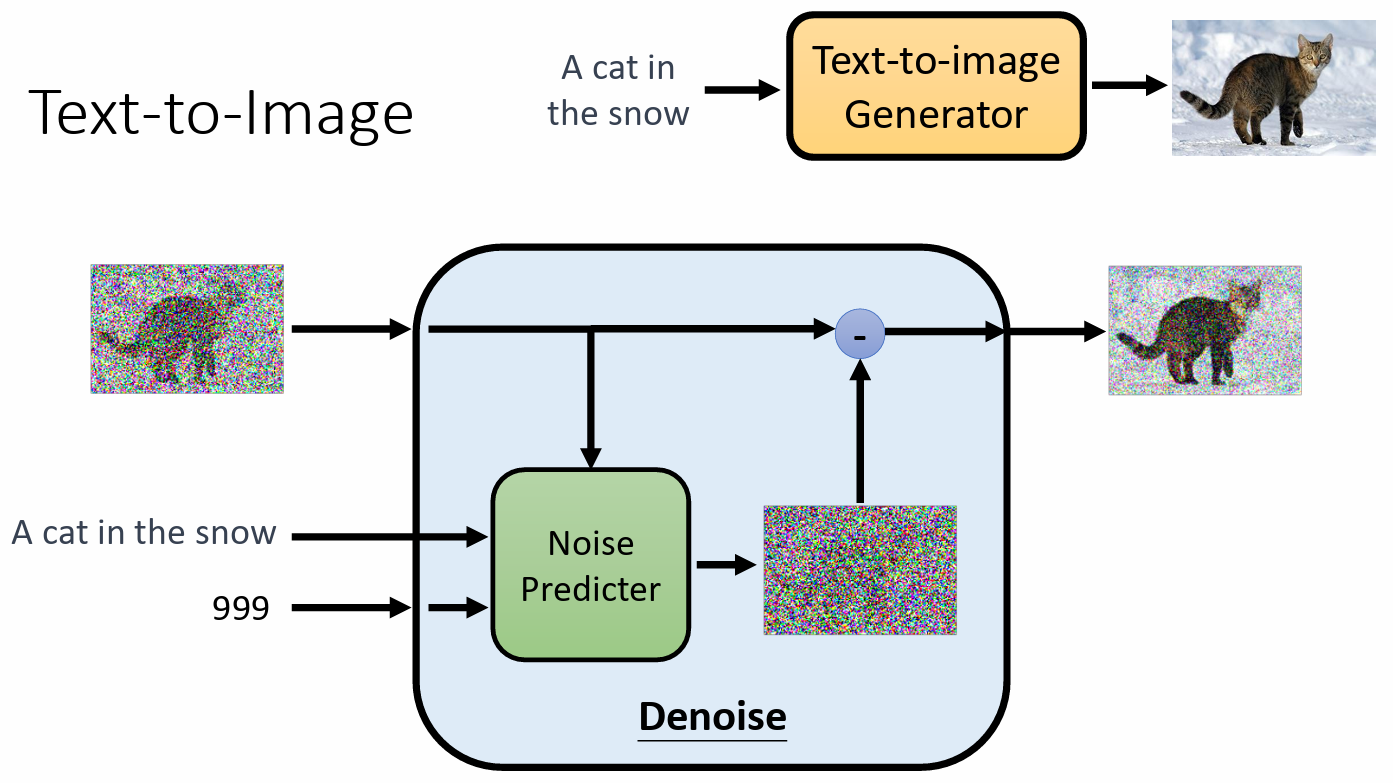
  • 生成图片的第一步： 生成 一个都是杂讯的图片，生成图片的大小和目标图片大小一致。
  • 然后进行 denoise，就是过滤掉先前图片中的部分杂讯
  • 不断进行 denoise，最后得到一张清晰的图片
  • 每一步 denoise 都有一个编号，越之后的步骤的 denoise 的编号越小

image-20240317212847637

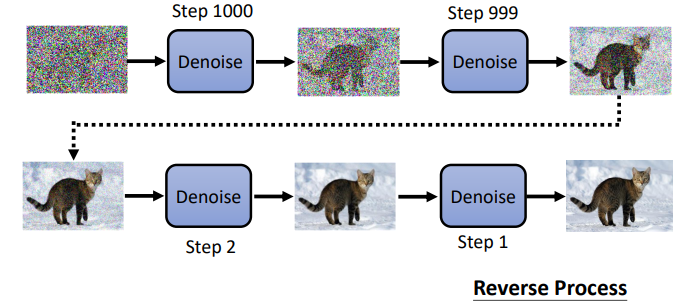
从杂讯到图片的过程称为 reverse process。

跟雕塑一样

denoise 的模型，除了需要输入一张图片之外，还要一个代表当前图片 noise 的程度的输入。

image-20240317212900743

Denoise 模组内部实际做的事情

denoise 模组内部有一个 noise predicter，预测图片中的杂讯长什么样，需要输入一张图片和图片的 noise 程度，然后输出一张输入图片的杂讯，减去输入图片，达到 denoise 的效果

image-20240317213434906

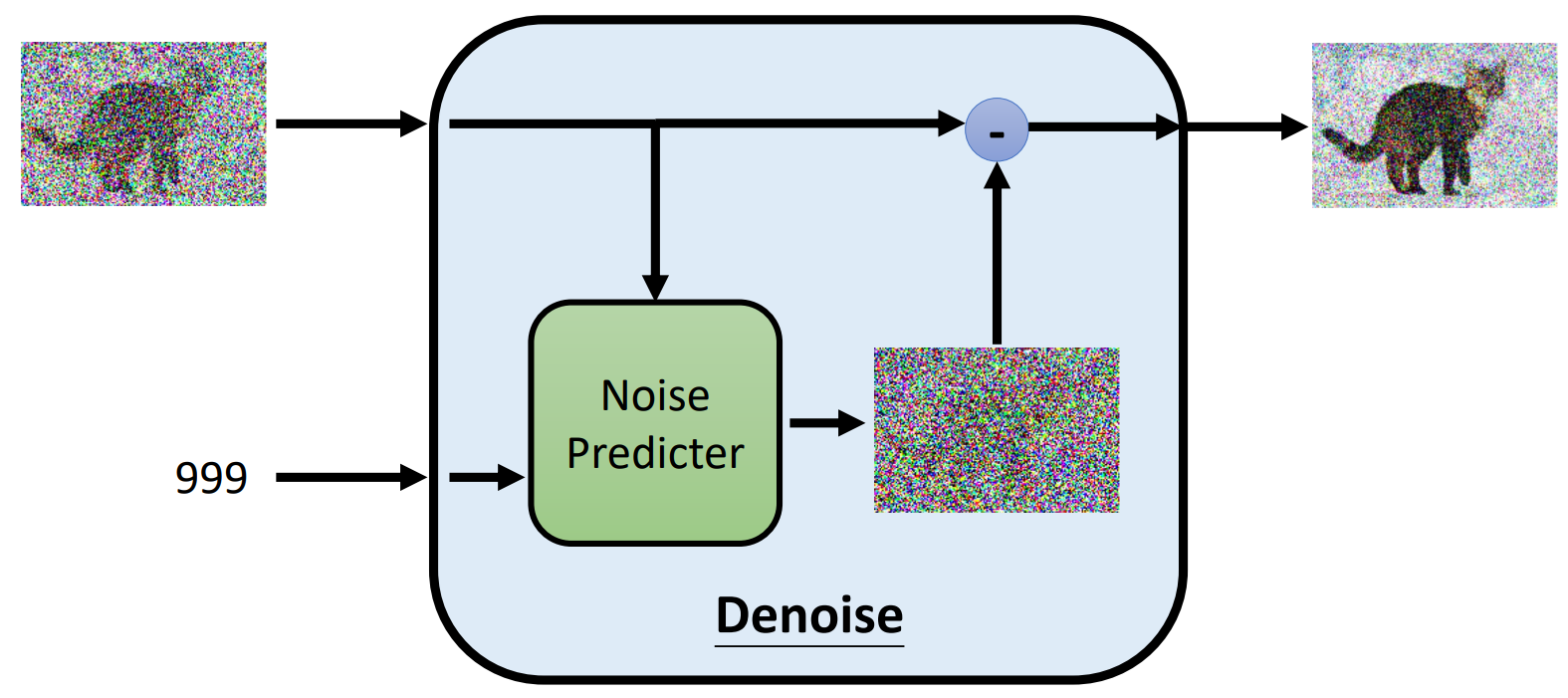
直接产生一张更清晰的图片比产生一种 noise 图片更难，所以现在大部分模型都会选择先产生一张 noise 的图片

如何训练 noise predictor?

image-20240317213645053

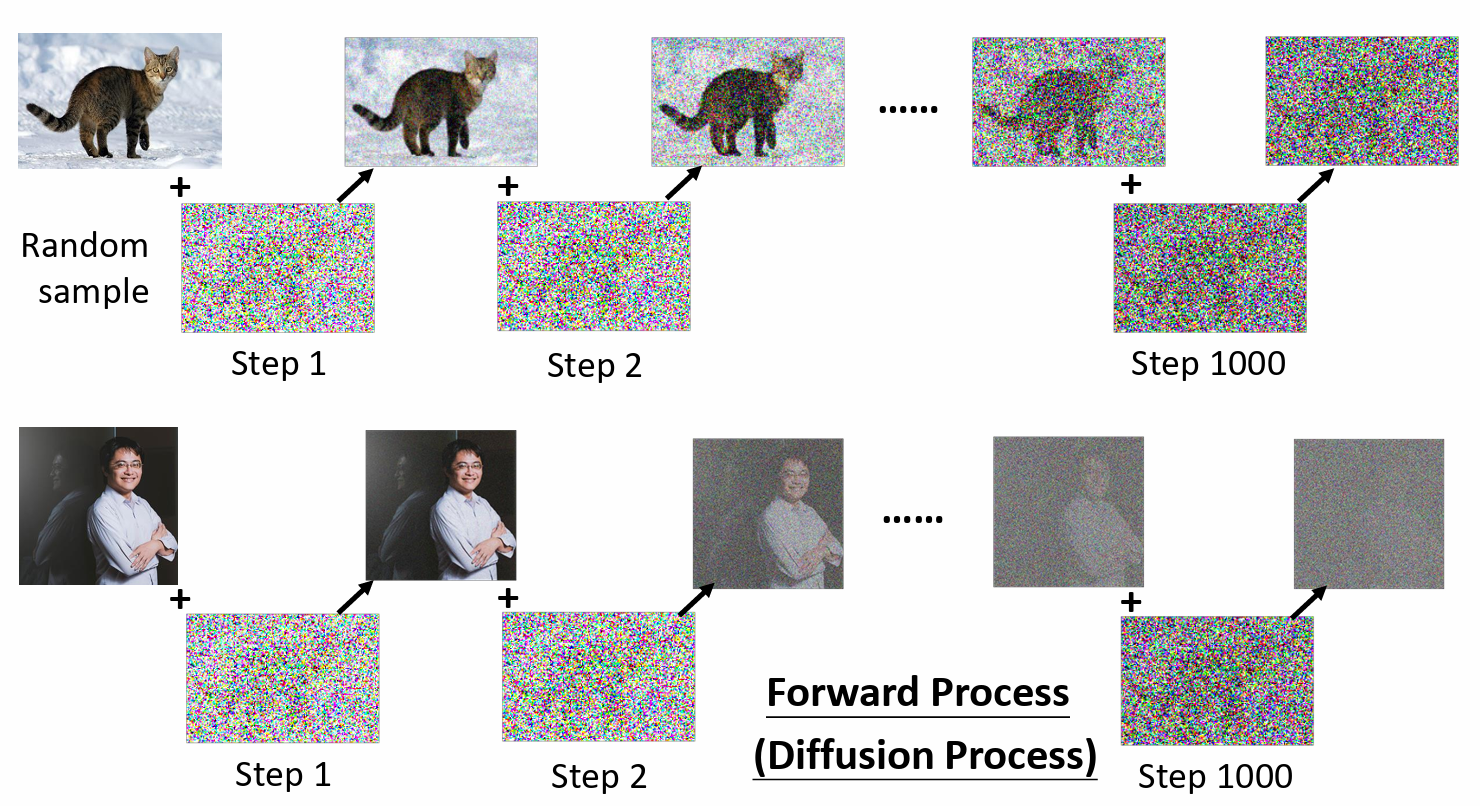
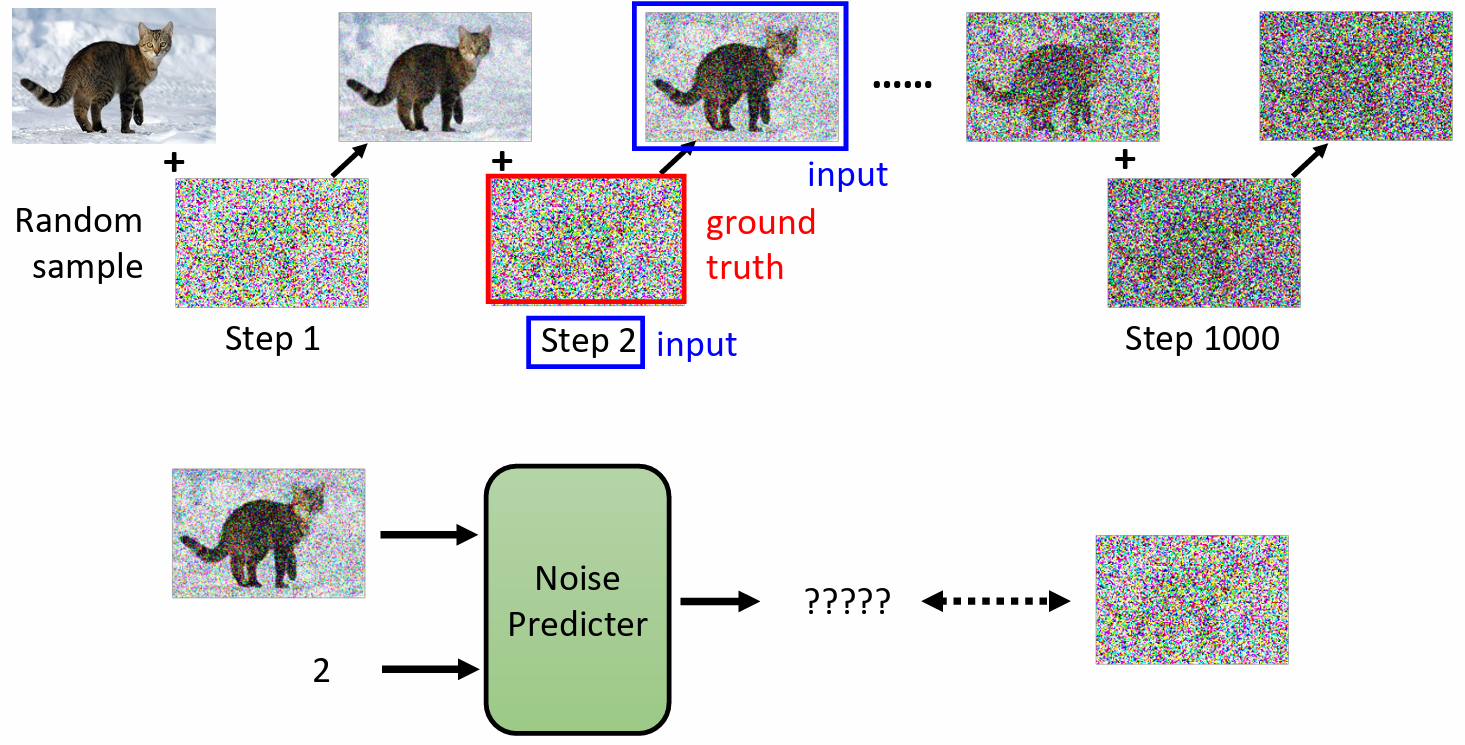
  • 对图片不断加 noise

  • 把某次加noise后的图片作为输入，对应的 noise 就是它的输出

    image-20240317213908476

Text-to-Image

  • 训练 文字-图片生成模型，需要文字-图片成对的资料
  • 大部分图片来源于 laion（网站?）
  • 在训练 denoise model 的时候，加入 文字

image-20240317214504330

Stable Diffusion

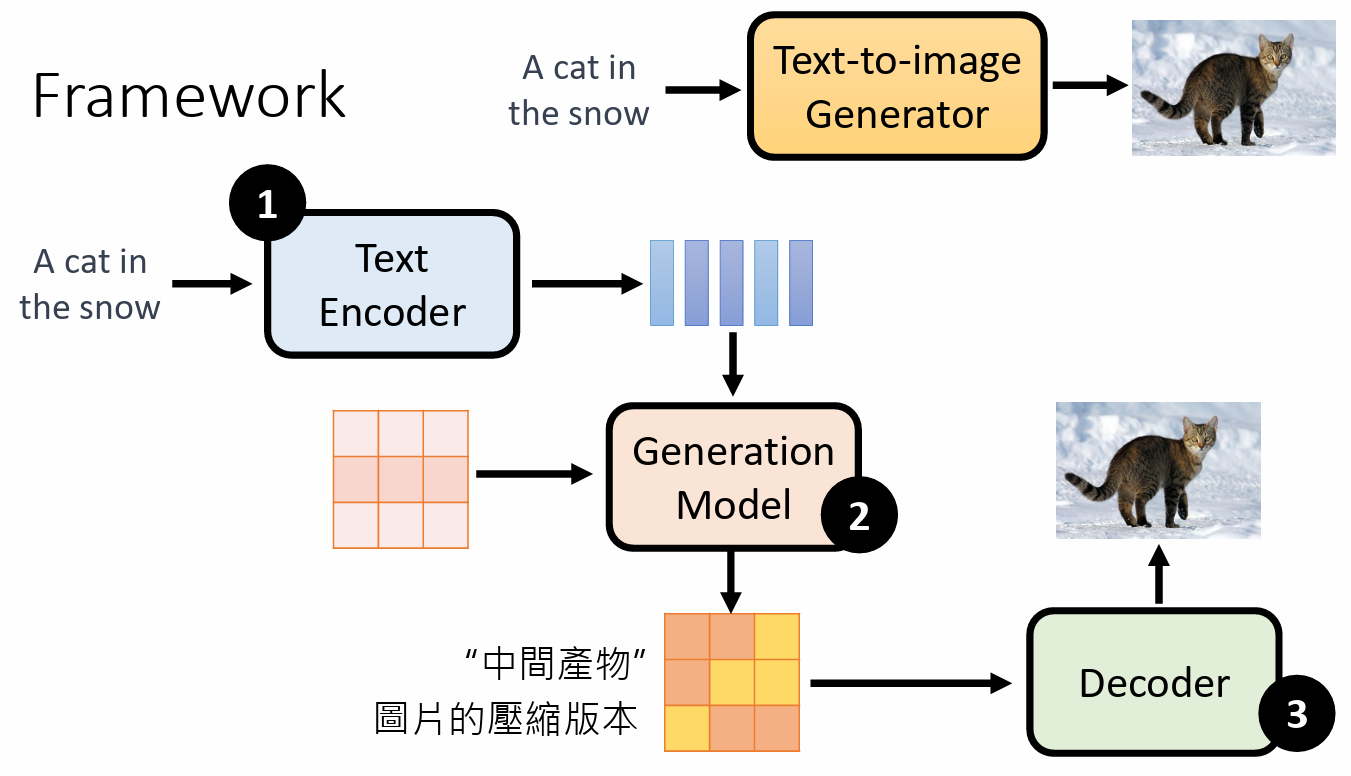
Framework

三个组成部分：

  • Text Encoder：文字叙述 编程 一个一个的向量

  • Generation Model：输入一个杂讯 和 文字的decoder译码结果，然后产生一个中间产物

    • 中间产物，是图片的压缩版本，可以是图片模糊的版本，也可以根本看不出来
  • Decoder：图片压缩版本还原成最终图片

三个组成部分是分开训练的，然后把他们组合起来的

image-20240317214846792

Stable Diffusion

image-20240317215256883

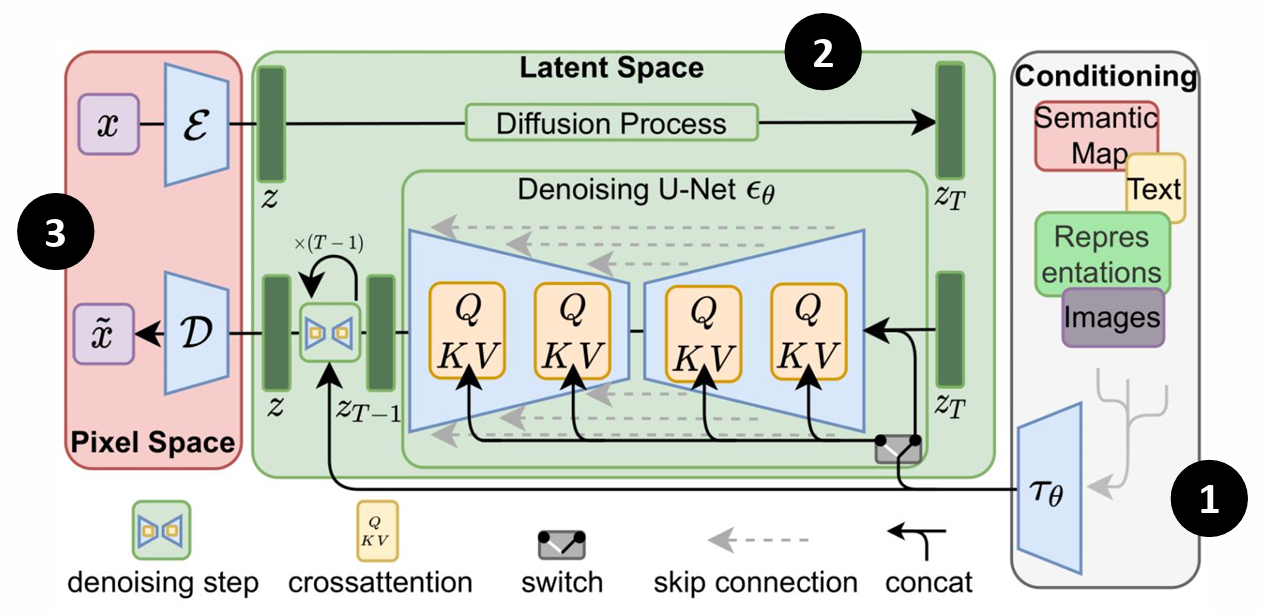
① 文字的译码器 Text Encoder

② 生成模型 generation model

③ 解码器 decoder

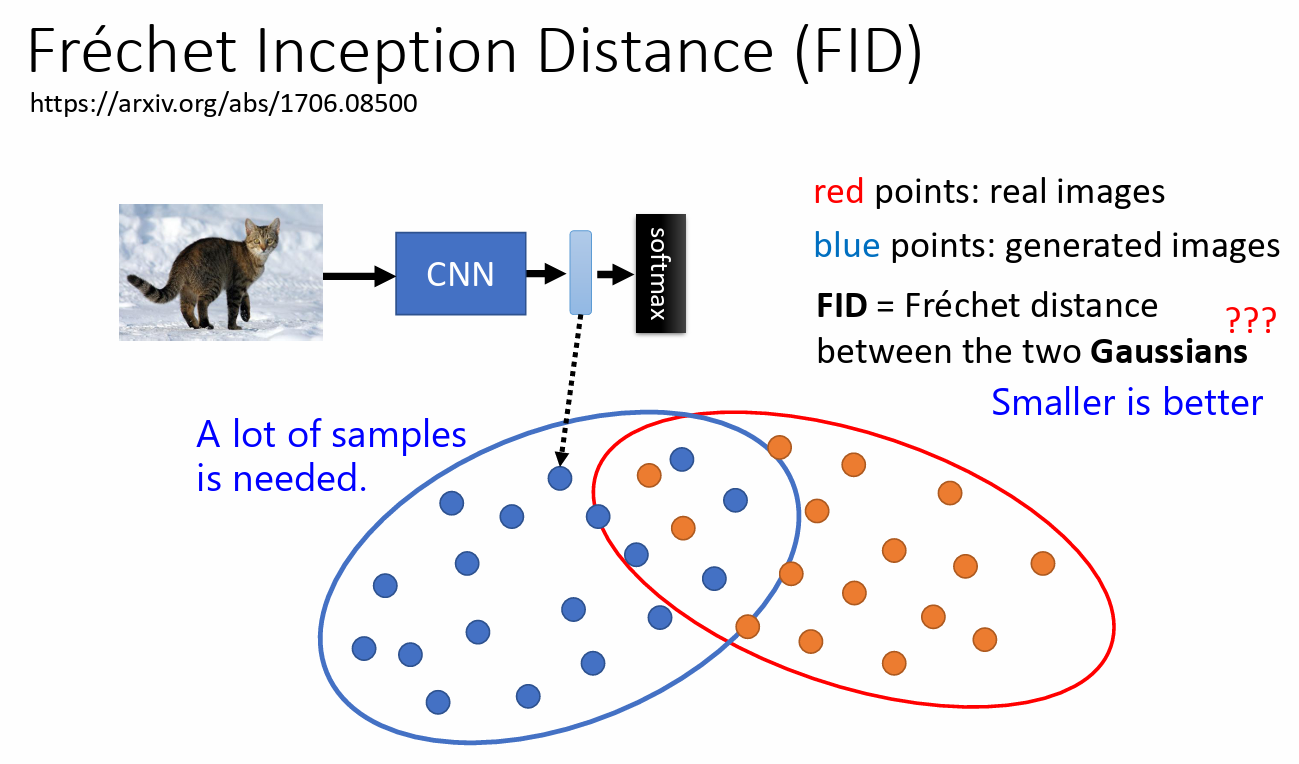
Fréchet Inception Distance(FID)

  • 现有一个 CNN model 和 影像分类的模型
  • 把真实图片和生成图片输入 CNN 模型中，产生 representation
  • 然后比较两组的 representation
  • 用来衡量图片生成好坏的模型
  • 需要大量的样本支撑
  • FID 是把图片当成 Gaussian 高斯图片，然后计算图片之间的距离
  • 真实图片和生成图片之间的距离越小越好

image-20240317220910746

Decoder

  • 训练 decoder 的时候不需要 文字 和 图片 的成对资料
  • 如果中间产物为小图，那么 decoder 的训练就是把一张图片的小图作为输入，然后生成大图

  • 如果中间产物是 Latent Representation，就是训练一个 latent encoder，让一张图片输入到latent encoder 中，然后把输出的 latent representation 通过 decoder 还原图片，两张图片越接近越好。就这样训练 decoder，训练完成之后就可以把 decoder 单独拿出来去解码 latent representation。

    image-20240317222445567

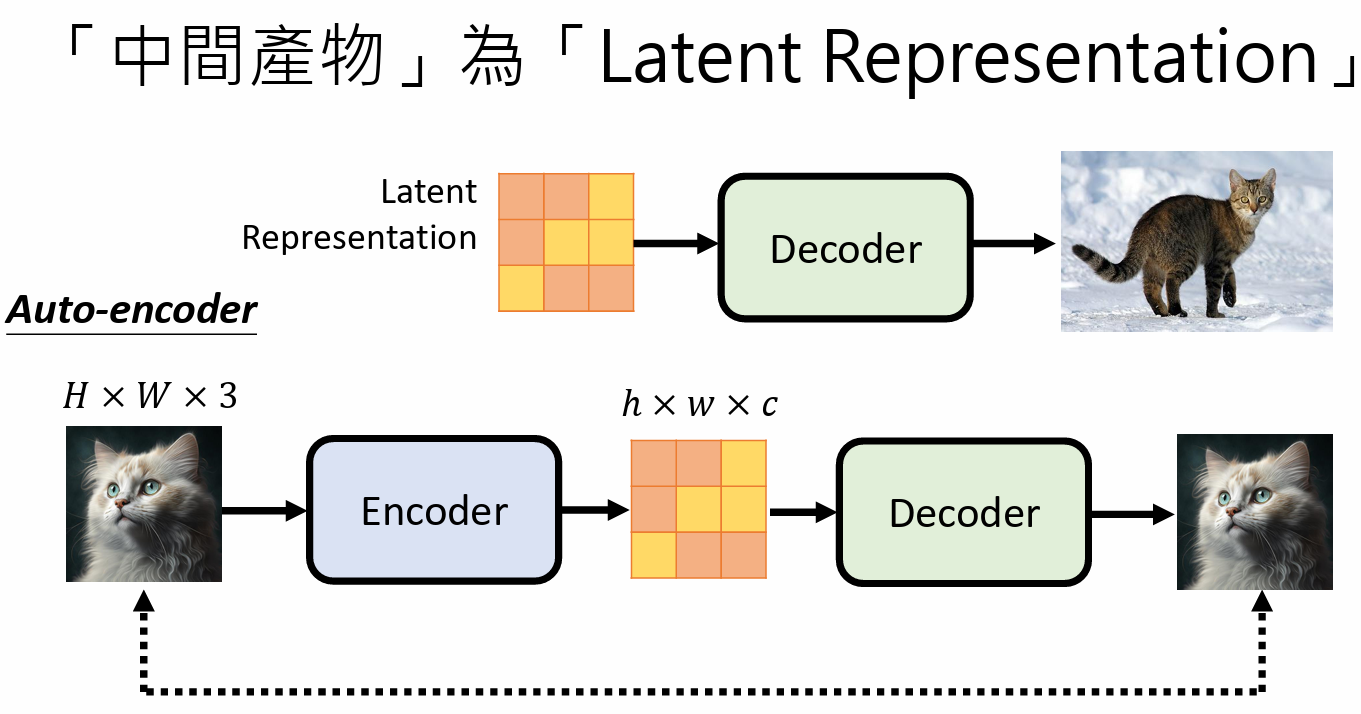
    如果输入图片是 $H\times W\times 3$ （H: height, W:width, 3: RGB），那么输出图片就可以认为是 $h\times w \times c$ ，它可以是人类看不懂的图片

Generation Model

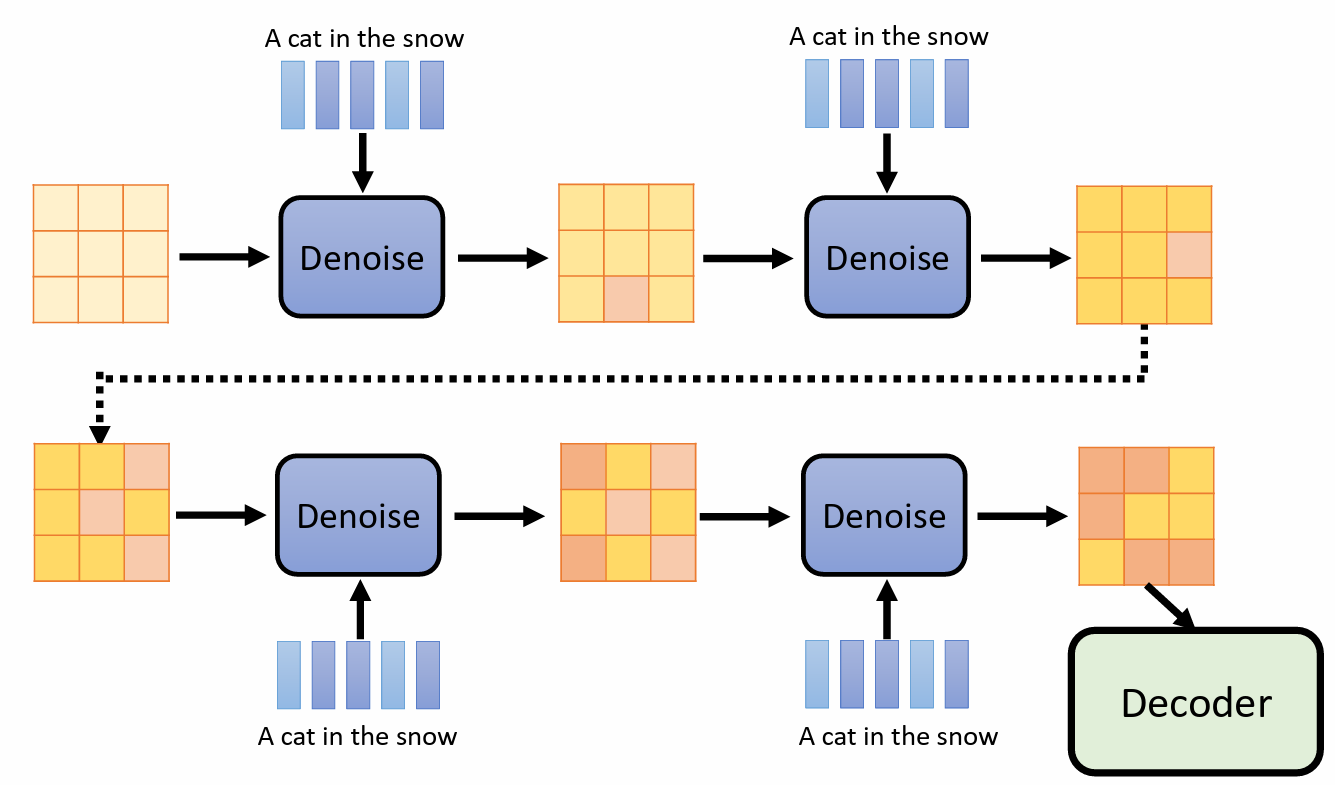
训练 Noise predicter：

  • 用一张图片和一个 encoder 产生一张 latent representation，再用杂讯加在 latent representation，不断加杂讯。

  • Noise Predicter的输入：

    • 加入杂讯后的 latent representation
    • step 编号的输入（代表和原来 latent representation 之间差距）
    • 文字的输入（文字是用一排向量表示，也是 latent representation）

image-20240317223524640

Diffusion Model 背后的数学原理

基本概念

  • Forward Process

    就是给一张图片，然后不断添加 noise

  • Reverse Process

    给一个全 noise 的 图片，每次 denoise，图片都会一点点浮现出来，到最后呈现的是完整的图片

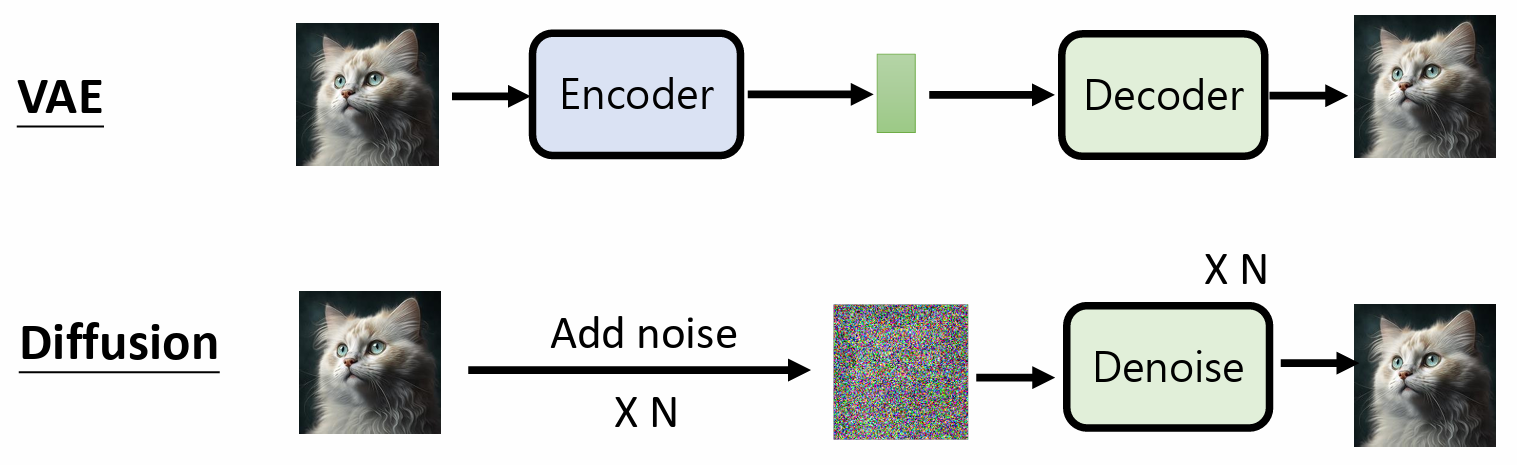
VAE vs. Diffusion Model

VAE

[photo] => Encoder => Latent Representation => Decoder => [photo]

Diffusion

[photo] => Add noise(固定好的，人设计的，不需要训练) => [只有杂讯的image] => denoise => [photo]

image-20240317225001693

Denoising Diffusion Probabilistic Models

image-20240317214625015

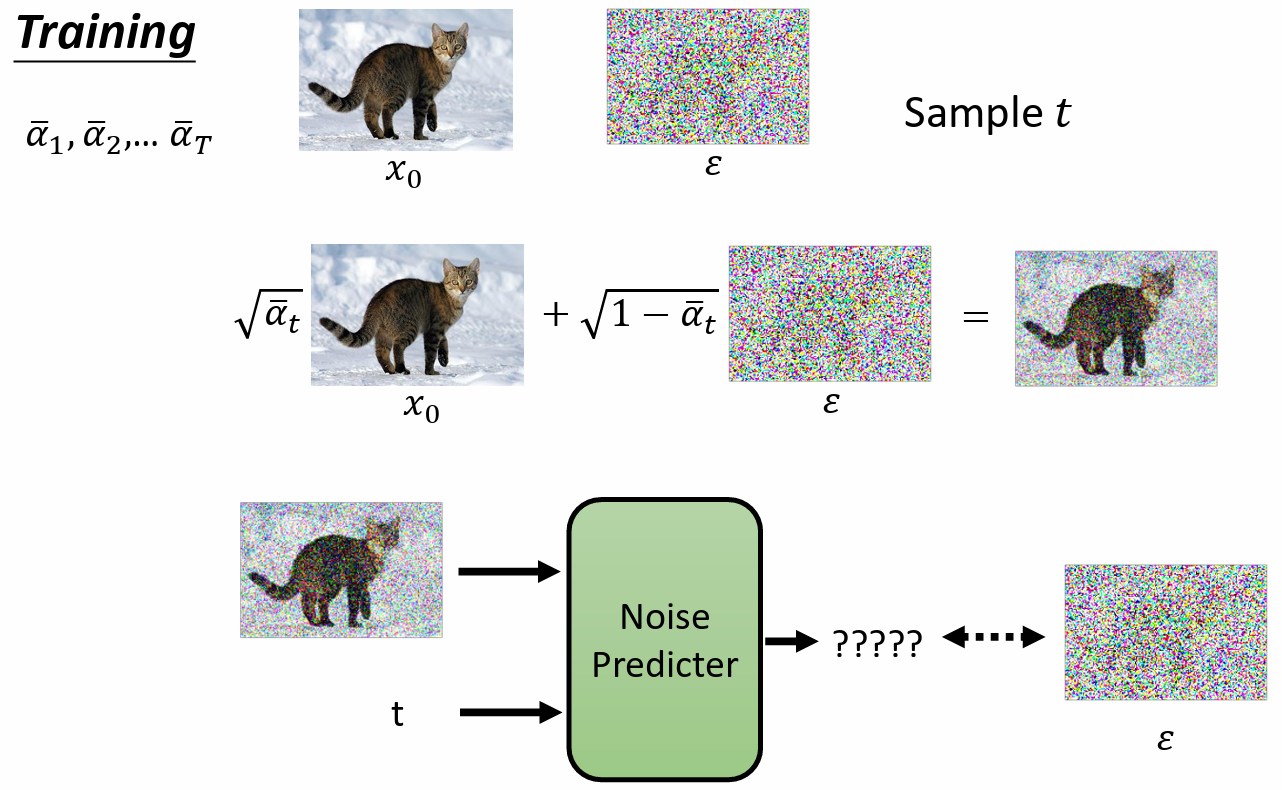
Training

  • 1： repeat 重复
  • 2：sample 一张 image $x_0$，$x_0$ 代表干净的图
  • 3：从一个较大数的范围内 sample 一个数字 $t$​ 出来
  • 4：$\epsilon$​ 是从 normal distribution 中训练出来的，sample a noise

  • 5：采取梯度下降法 $ \nabla_{\theta} \Vert \epsilon - \epsilon_{\theta}(\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon, t)\Vert$

    • $\epsilon$ ：target noise
    • $\epsilon_{\theta}$：noise predictor
    • t 越大，$\bar{\alpha}_t$ 越小，离 $x_0$ 越远，离 target noise $\epsilon$ 越近

image-20240317225548205

image-20240317231527242

image-20240317231747484

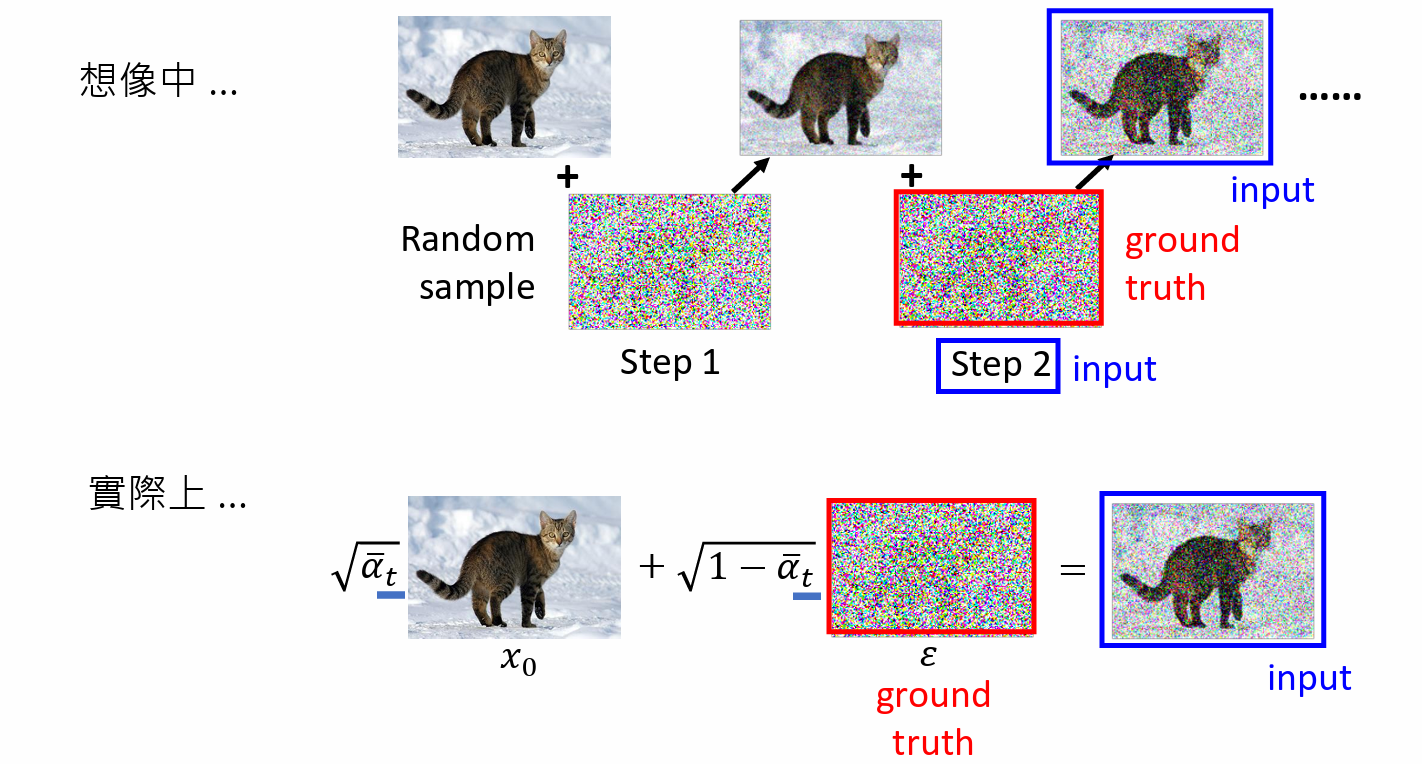
实际上：

  • 干净图直接混入一个噪音，通过 $\bar\alpha_t$ 直接决定噪音的大小，得到一个有噪音的图
  • 训练的时候，把有噪音的图 和 t 当作输入，直接预测 混入的 噪音

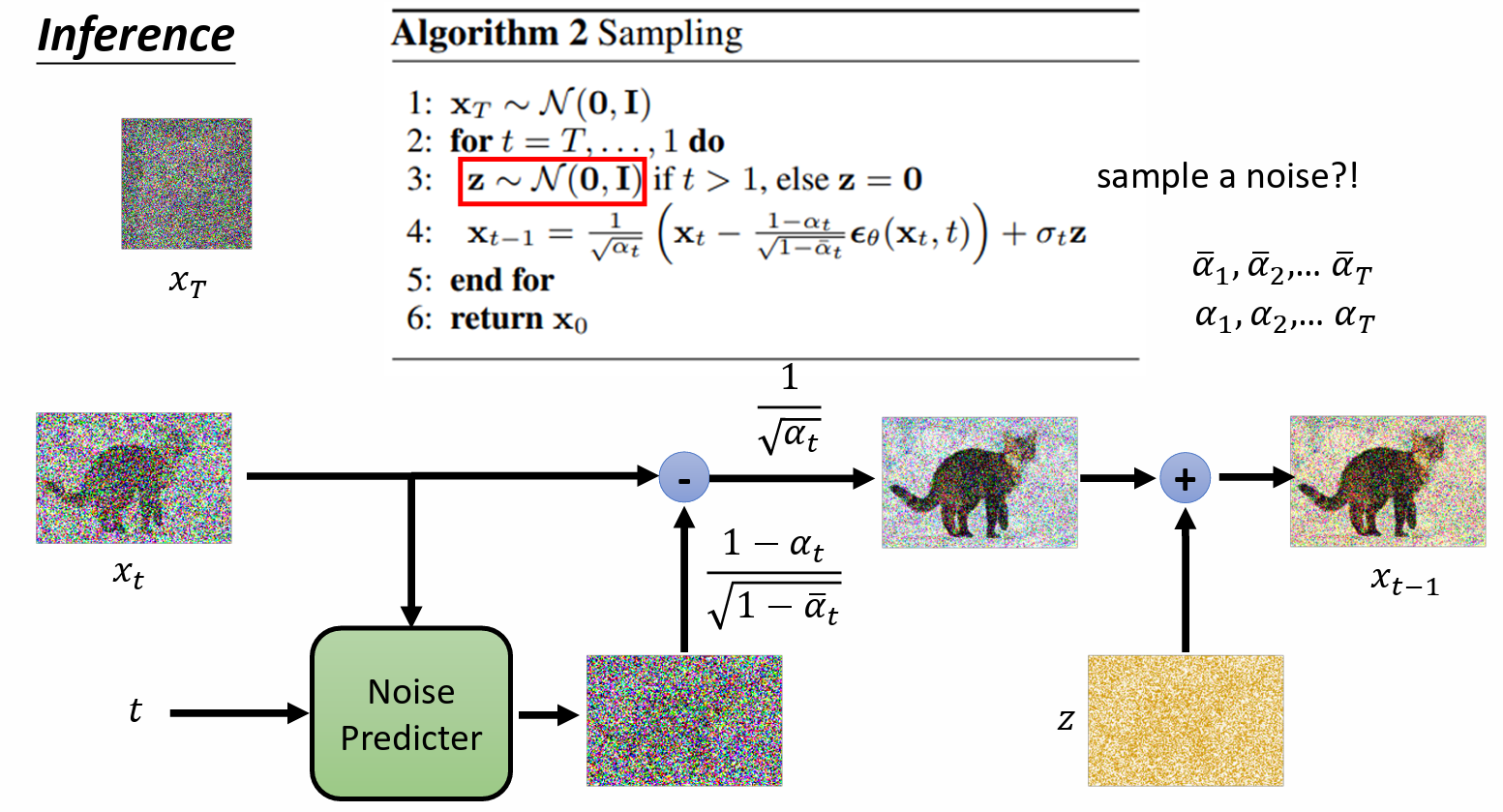
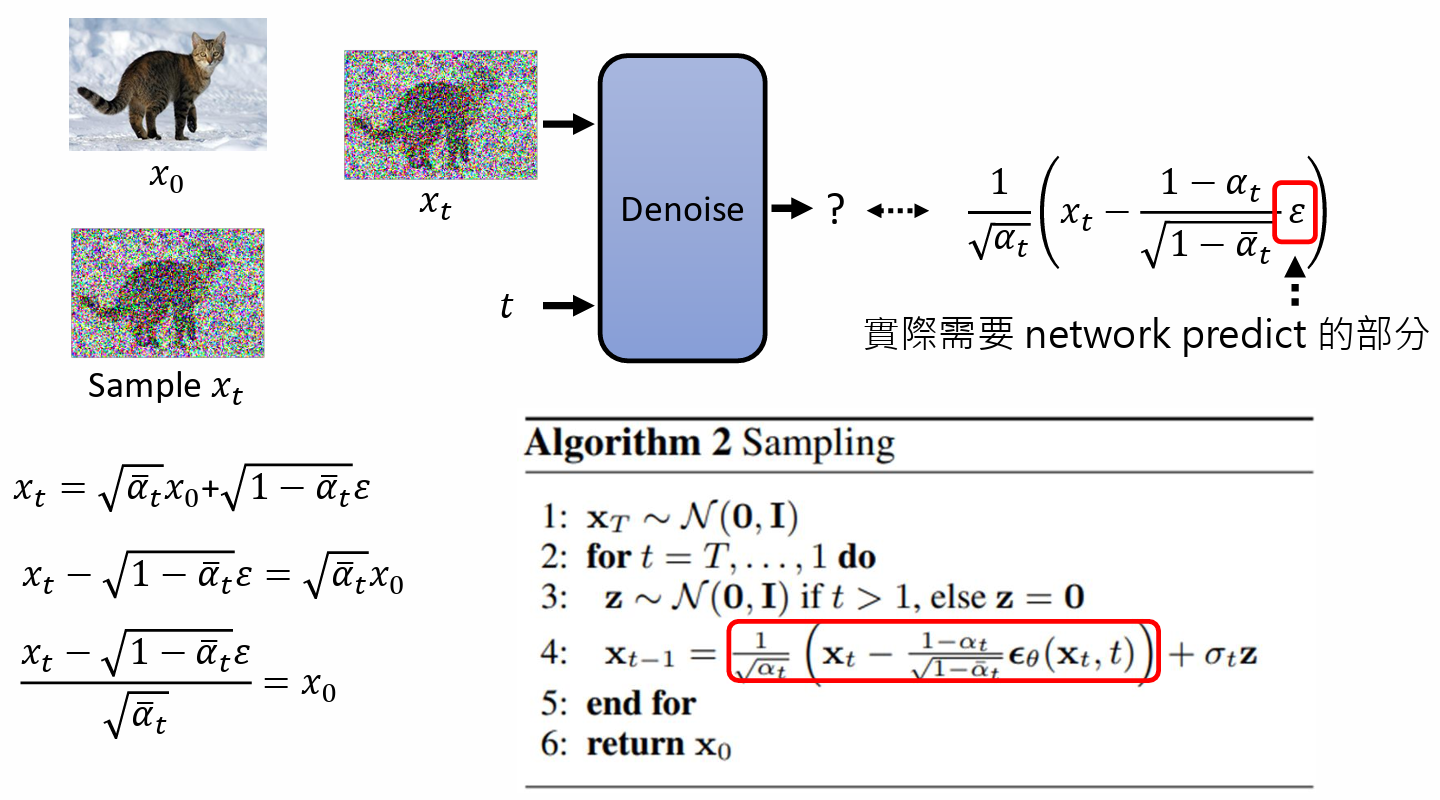
Sampling

产生图片的过程：

  1. 一开始，sample 一个全是 noise 的图 $x_T$

  2. 运行 T 次，t = T, ..., 1 do

    1. 再 sample 一次 noise $\boldsymbol{z}$

    2. $\boldsymbol{x}_{t-1} = \cfrac{1}{\sqrt{\alpha}_t}\big(\boldsymbol{x}_t - \cfrac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon_{\theta}(\boldsymbol{x}_t, t)\big) + \sigma_t \boldsymbol{z}$​

      • x_t 是上一个步骤产生出来的图
      • $\epsilon_{\theta}$ 是 noise predicter 输出的 noise

image-20240317232444773

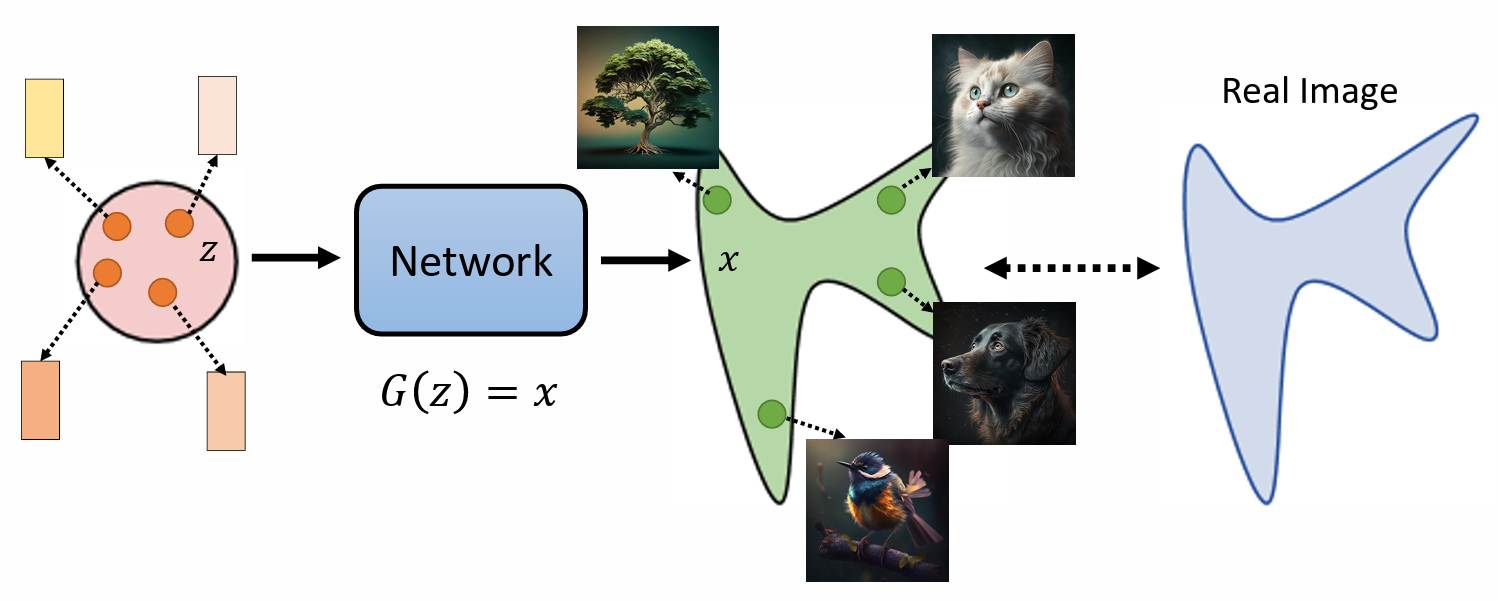
影像生成模型本质上的共同目标

  • Gaussian distribution：正态分布
  • 在 input 的地方有一个简单的 distribution，通常是 Gaussian distribution（正态分布）
  • 从 input 的地方 sample 一个东西出来，通常是 vector，然后把这个 vector 放在 network 里面去， $G(z) = x$​ ，z 表示输入，x 就是一张图片
  • 每次从 input 的地方 sample 一个 vector 出来，通过 network 就变成一张图片。
  • 就算输入是非常简单的 Gaussian distribution ，通过 network 转换，输出会变成一张张图片，这些图片会组合成非常复杂的 distribution。

  • 我们期待的事情是，我们找到一个 network，这个 network 应该做到的事情是跟真正的图片的 distribution 和真正图片所形成的 distribution 越接近越好。

    image-20240317235615207

Maximum Likelihood Estimation

  • 什么叫做越接近越好？

    • 大部分利用 Maximum Likelihood Estimation 判断

  • 假设 network 的参数为 $\theta$ ，然后根据 $\theta$ 产生的 distribution 表示为 $P_\theta(x)$，真正的 distribution 表示为 $P_{data}(x)$ （Maximum Likelihood Estimation）

    • 首先从 $P_{data}(x)$ 中 sample 一堆 image $\{x^1, x^2, ..., x^m\}$ 出来

      • $P_{data}(x)$​ 是所有可能搜集到的训练资料
    • 假设我们能够计算 $P_\theta(x^i)$
    • 我们要找$\theta$ 是 $\theta^* = arg \max_\theta\prod^m_{i=1}P_\theta(x^i)$​

    使得产生 $x^1, x^2, \cdots, x^m$ 这些图片的概率的乘积最大

    Sample $\{x^1, x^2, \dots, x^m\}$ from $P_{data}(x)$

    $$ \begin{align} \theta^* &= arg\max_\theta\prod^m_{i=1}P_\theta(x^i) = arg\max_\theta\log\prod^m_{i=1}P_\theta(x^i)\\ &= arg\max_\theta\sum^m_{i=1}\log P_\theta(x^i) \approx arg\max_\theta E_{x\sim P_{data}}[\log P_\theta (x)] \\ &= arg\max_\theta \int_x P_{data}(x)\log P_\theta (x) \mathrm{dx} - \int_x P_{data}(x)\log P_{data} (x)\mathrm{dx}\\ &= arg\max_\theta \int_x P_{data}(x)\log \cfrac{P_\theta (x)}{P_{data} (x)} \mathrm{dx} \\ &= arg \min_\theta KL(P_{data}\Vert P_\theta) \end{align} $$

    • KL Divergence 计算两个 distribution 的差异程度

      $KL(P_{data}\Vert P_\theta)$ ：Difference between $P_{data}$ and $P_\theta$​

      越大，差异越大

    • Maximum Likelihood = Minimize KL Divergence

image-20240318130635125

VAE

Compute $P_\theta(x)$

  • z => network => G(z) = x (arg = $\theta$) => 计算 $P_\theta(x)$

  • VAE 假设 输入 z，输出 G(z)，G(z) 代表 Mean of Gaussian

    所以 $P_\theta(x|z) \propto \exp(-\Vert G(z) - x\Vert_2)$​

    • $\Vert G(z) - x\Vert_2$ 表示 $G(z)$ 和输入数据 $x$ 之间的欧氏距离

Lower bound of $\log P(x)$

$$ \begin{align} \log P_\theta(x) & = \int_z q(z|x) \log P(x) \mathrm{dz}\\ &= \int_z q(z|x) \log\bigg(\cfrac{P(z,x)}{P(z|x)}\bigg)\mathrm{dz} = \int_z q(z|x) \log\bigg(\cfrac{P(z,x)}{q(z|x)}\cfrac{q(z|x)}{P(z|x)}\bigg)\mathrm{dz}\\ &= \int_z q(z|x) \log\bigg(\cfrac{P(z,x)}{q(z|x)}\bigg)\mathrm{dz}+\int_z q(z|x) \log\bigg(\cfrac{q(z|x)}{P(z|x)}\bigg)\mathrm{dz}\\ & \geqslant \int_z q(z|x)\log \bigg(\cfrac{P(z,x)}{q(z|x)}\bigg)\mathrm{dz} = \mathrm{E}_{q(z|x)}[\log\bigg(\cfrac{P(z,x)}{q(z|x)}\bigg)] \end{align} $$

  • 因为logP(x)与z无关，所以可以提出积分外面，那么积分里面的东西，积完以后就是1，右边跟左边一样，所以 $\log P_\theta(x)$ 与 $q(z|x)$​ 无关
  • $\int_z q(z|x) \log\bigg(\cfrac{q(z|x)}{P(z|x)}\bigg)\mathrm{dz} = KL(q(z|x)\Vert P(z|x)) \geqslant 0$
  • $\log P_\theta(x)$ 的 lower bound 是 $\mathrm{E}_{q(z|x)}[\log\bigg(\cfrac{P(z,x)}{q(z|x)}\bigg)]$
  • 如果可以 Maxmize 这个 lower bound，就可以使得 $\log P(x)$​​ 得到一个较大的值
  • 在 VAE 中，$\mathrm{E}_{q(z|x)}$ 就是 Encoder

DDPM

Compute $\log P_\theta(x)$

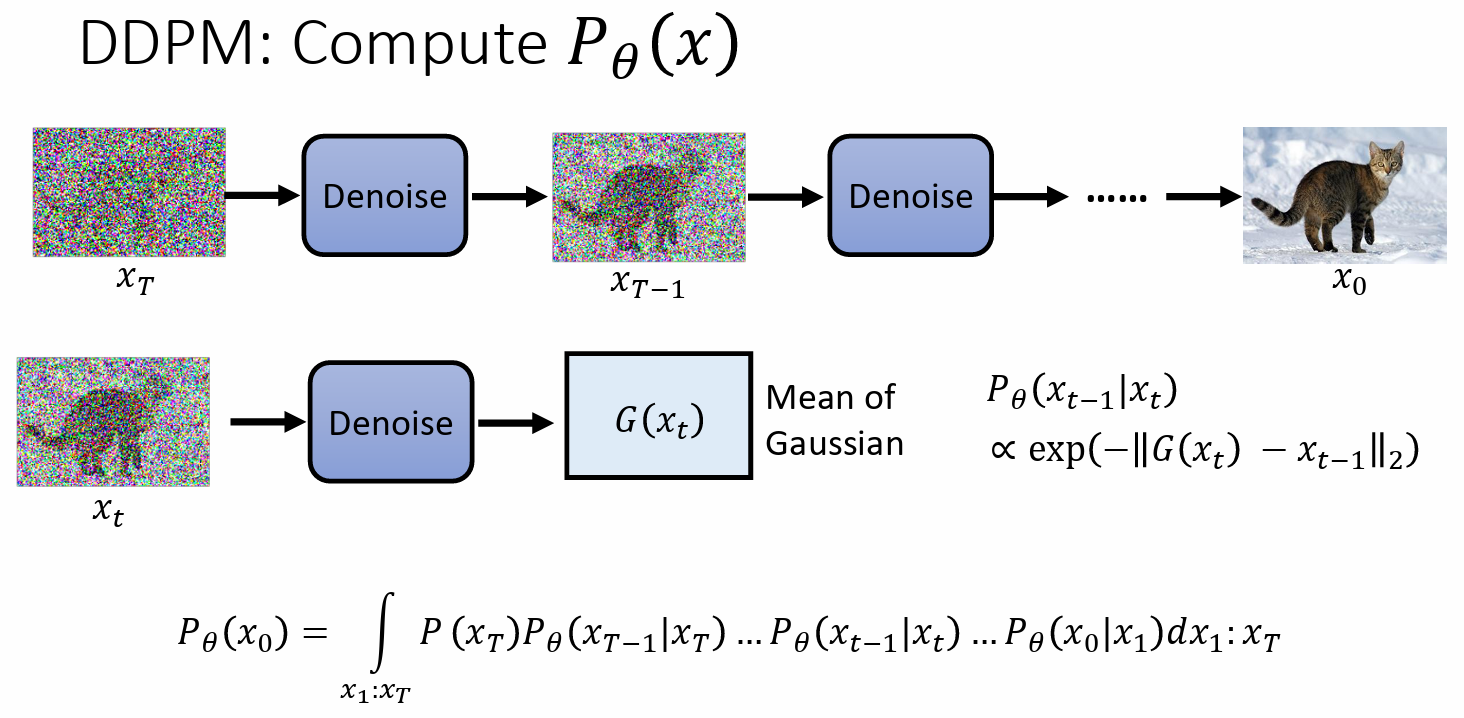
  • 可以把 denoise 的过程想成产生 Gaussian distribution，当输入 $x_t$ 输入 denoise model，就会产生一个 结果 $G(x_t)$​ ，把这个 output 的结果想成 Mean of Gaussian。
  • 如果 $x_{t-1}$​ 和 output 的结果正好一模一样，是几率最大的 case，如果差很远，几率就小很多

  • $P_\theta(x_0) = \int_{x_1: x_T} P(x_T)P_\theta(x_{T-1}|x_T)...P_\theta(x_{t-1}|x_t)...P_\theta(x_0|x_1) \mathrm{dx_1:x_T}$

    对所有可能的 $x_1: x_T$​​ 做积分

    image-20240318190653290

Lower bound of $\log P(X)$

  • VAE: Maximize $\log P_\theta(x)$ => Maximize $\mathrm{E}_{q(z|x)}[\log \bigg(\cfrac{P(x,z)}{q(z|x)}\bigg)]$​

    • $q(z|x)$ 是 Encoder

  • DDPM Maximize $\log P_\theta(x_0)$ => Maximize $\mathrm{E}_{q(x_1:x_T|x_0)}[\log \bigg(\cfrac{P(x_0:x_T)}{q(x_1:x_T|x_0)}\bigg)]$​

    • $q(x_1:x_T|x_0)$​ 是 Forward Process（Diffusion Process）

      就是加 noise 的过程

    • $q(x_1:x_T|x_0) = q(x_1|x_0)q(x_2|x_1)...q(x_T|x_{T-1})$

计算 $q(x_t|x_{t-1})$

  • $x_1 = \sqrt{1-\beta_1}x_0 + \sqrt{\beta_1}\ noise1, noise1\sim\mathcal{N}(0,I)$
  • $x_2 = \sqrt{1-\beta_2}x_1 + \sqrt{\beta_2}\ noise2, noise2\sim\mathcal{N}(0,I)$
  • noise1 和 noise2 都是从同样的高斯分布 Gaussian distribution 采样 sample 出来，但是这两次 sample 是相互独立

  • 可以把 $x_1$ 代入 $x_2$ 的公式中，得到

    $x_2 = \sqrt{1-\beta_2}\sqrt{1-\beta_1}x_0 + \sqrt{1-\beta_2}\sqrt{\beta_1}noise1 + \sqrt{\beta_2}\ noise2$

    $noise1,noise2\sim\mathcal{N}(0,I)$​

    $\sqrt{1-\beta_2}\sqrt{\beta_1}noise1 + \sqrt{\beta_2}\ noise2 = \sqrt{1-(1-\beta_2)(1-\beta_1)}noise$

    $noise\sim \mathcal{N}(0, I)$​

    所以，$x_2 = \sqrt{1-\beta_2}\sqrt{1-\beta_1}x_0 + \sqrt{1-(1-\beta_2)(1-\beta_1)}noise$​​

    image-20240318201025284

    image-20240318201000518

  • 以此类推，$x_t = \sqrt{1-\beta_1}...\sqrt{1-\beta_t} x_0 + \sqrt{1-(1-\beta_1)...(1-\beta_t)}noise$​

  • $\alpha_t = 1-\beta_t, \bar\alpha_t = \alpha_1\alpha_2...\alpha_t$

    则 $x_t = \sqrt{\bar\alpha_t} x_{t_0} + \sqrt{1-\bar\alpha_t} noise$​

Lower bound of $\log P(x)$ ：

$$ E_{q(x_1|x_0)}[\log P(x_0|x_1)]-KL(q(x_T|x_0)\Vert P(x_T))-\sum^T_{t=2}\mathrm{E}_{q(x_t|x_0)}[KL(q(x_{t-1}|x_t,x_0)\Vert P(x_{t-1}|x_t))] $$

how to maximize $\sum^T_{t=2}\mathrm{E}_{q(x_t|x_0)}[KL(q(x_{t-1}|x_t,x_0)\Vert P(x_{t-1}|x_t))]$

  • $q(x_{t-1}|x_t, x_0)$ ，从 $x_0$ 做了n次diffusion生成 $x_t$ ，求 $x_{t-1}$ 的分布（中间过程未知）

    $$ \begin{align} q(x_{t-1}|x_t, x_0) &= \cfrac{q(x_{t-1}, x_t, x_0)}{q(x_t, x_0)} = \cfrac{q(x_t|x_{t-1})q(x_{t-1}|x_0)q(x_0)}{q(x_t|x_0)q(x_0)} \\&= \cfrac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)} \end{align} $$

image-20240318203801769

image-20240318203923450

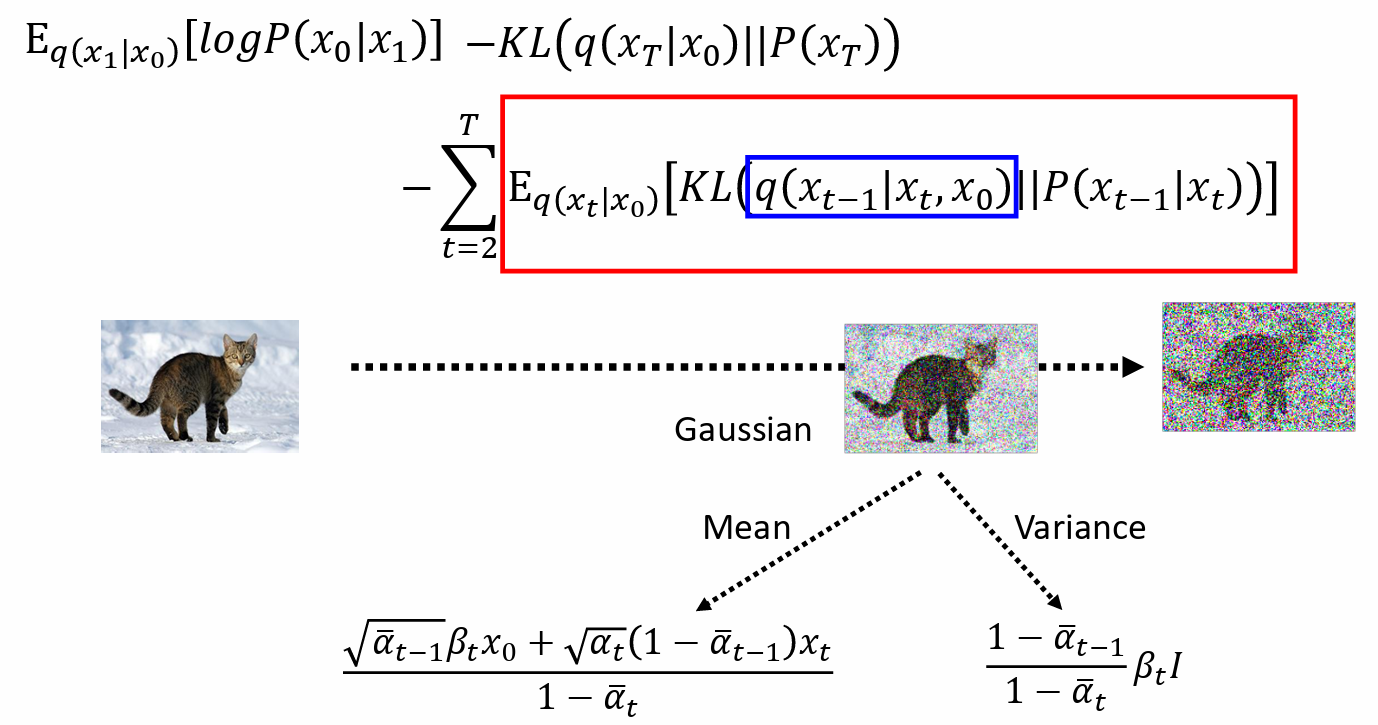
  • 我们不需要把 KL 算出来，我们只需要 minimize KL divergence
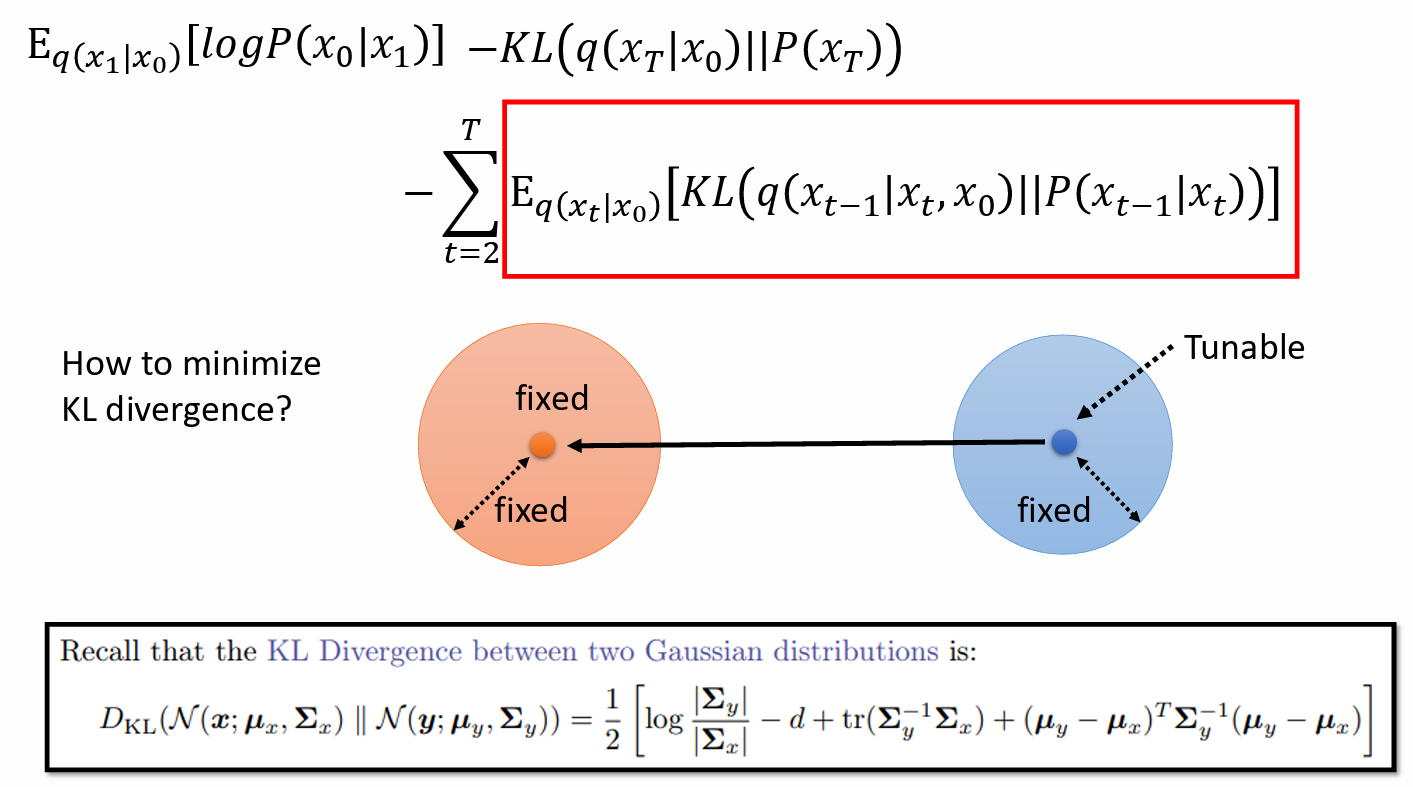
  • $q(x_{t-1}|x_t, x_0)$ 是固定的高斯分布 Gaussian distribution，和 network 没有关系，mean 是固定的，variance 是固定的。
  • $P(x_{t-1}|x_t)$ 是 由 network 决定，它的 variance 是固定的，只考虑 mean，mean 取决于 denoise model

image-20240318204401772

image-20240318204459454

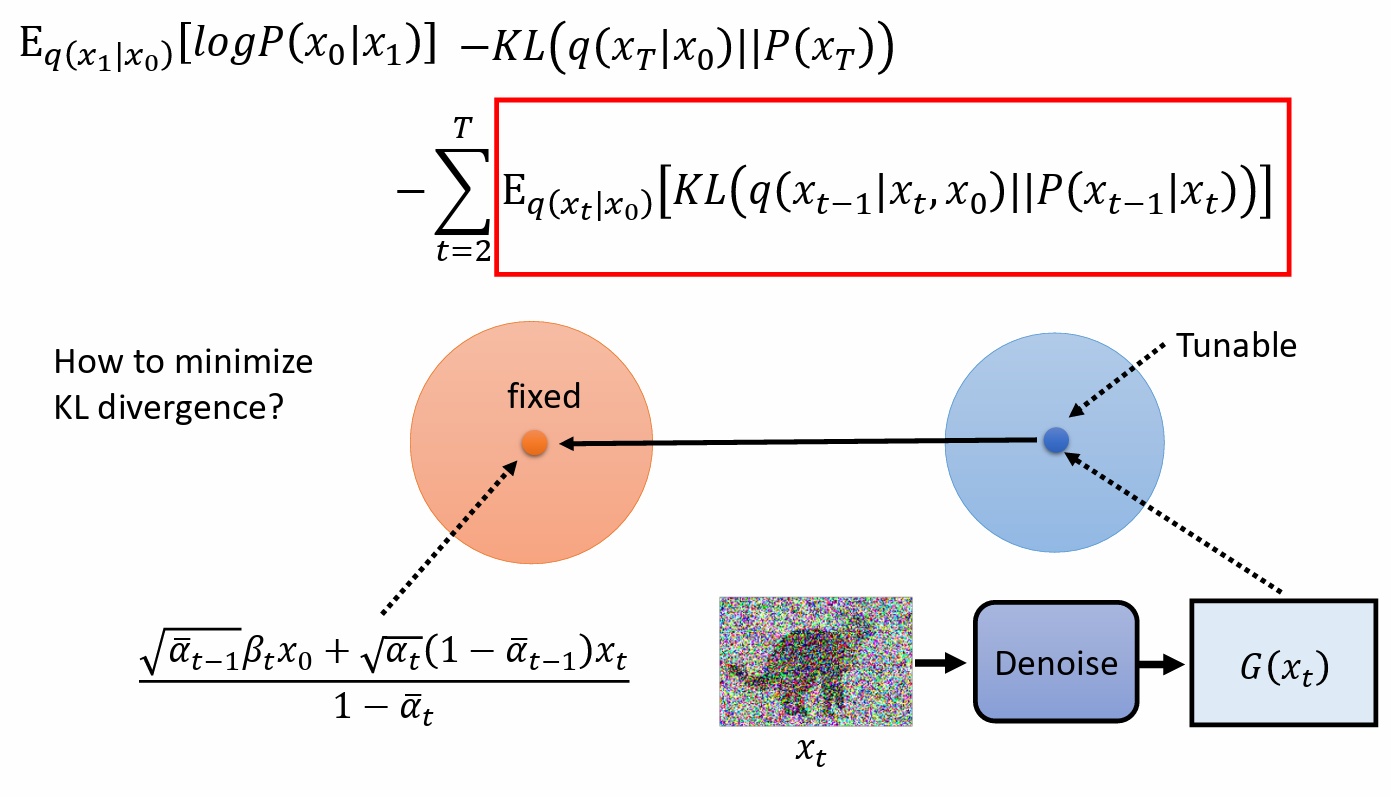
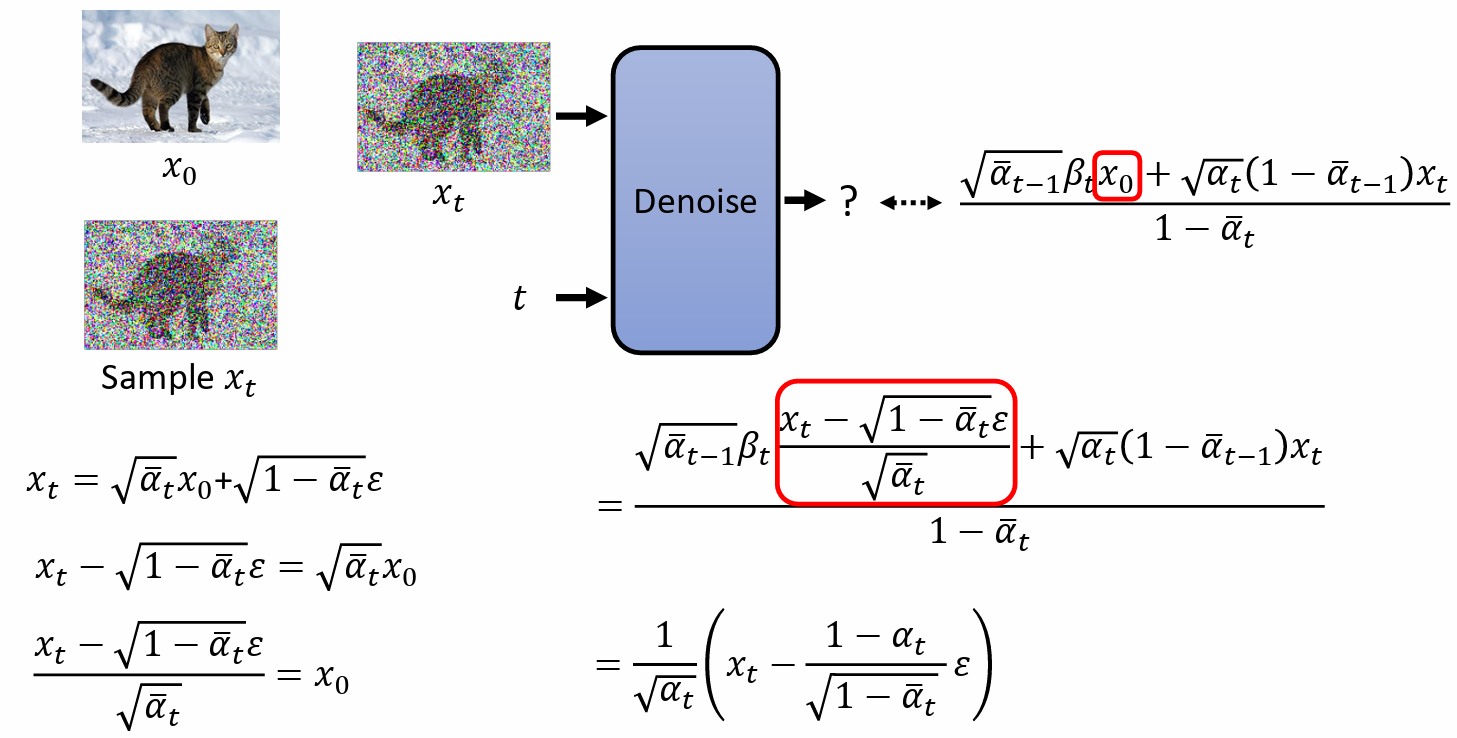
  • $x_0$​ 是先给定的

    通过 $x_t = \sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t}\epsilon$ sample 出 $x_t$​​

    image-20240318205012775

    image-20240318205037252

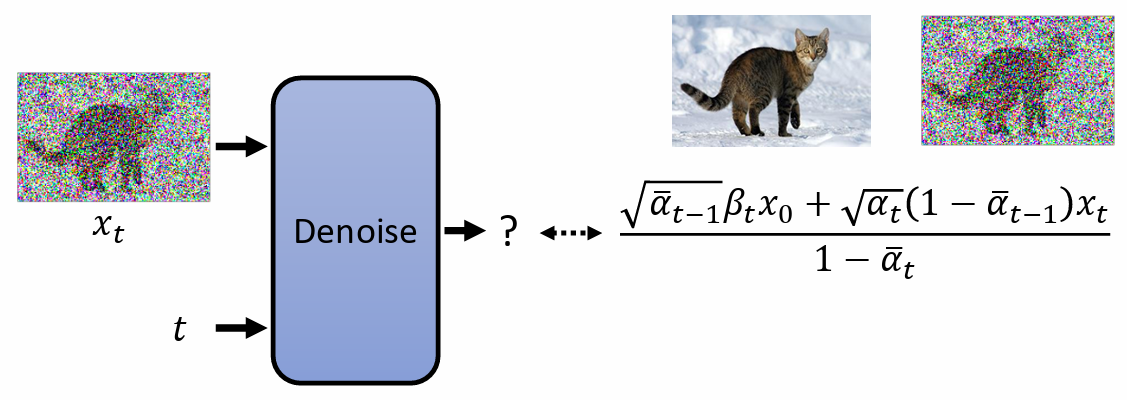
  • $x_t = \sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t}\epsilon$ => $\cfrac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}} = x_0$

    image-20240318205359912

    image-20240318205540071

Diffusion Model for Text

  • difficulty: 难以在文字这种 description 上加 noise

  • Solution：

    • 不在文字上加 noise

      Noise on latent space

      image-20240318213703294

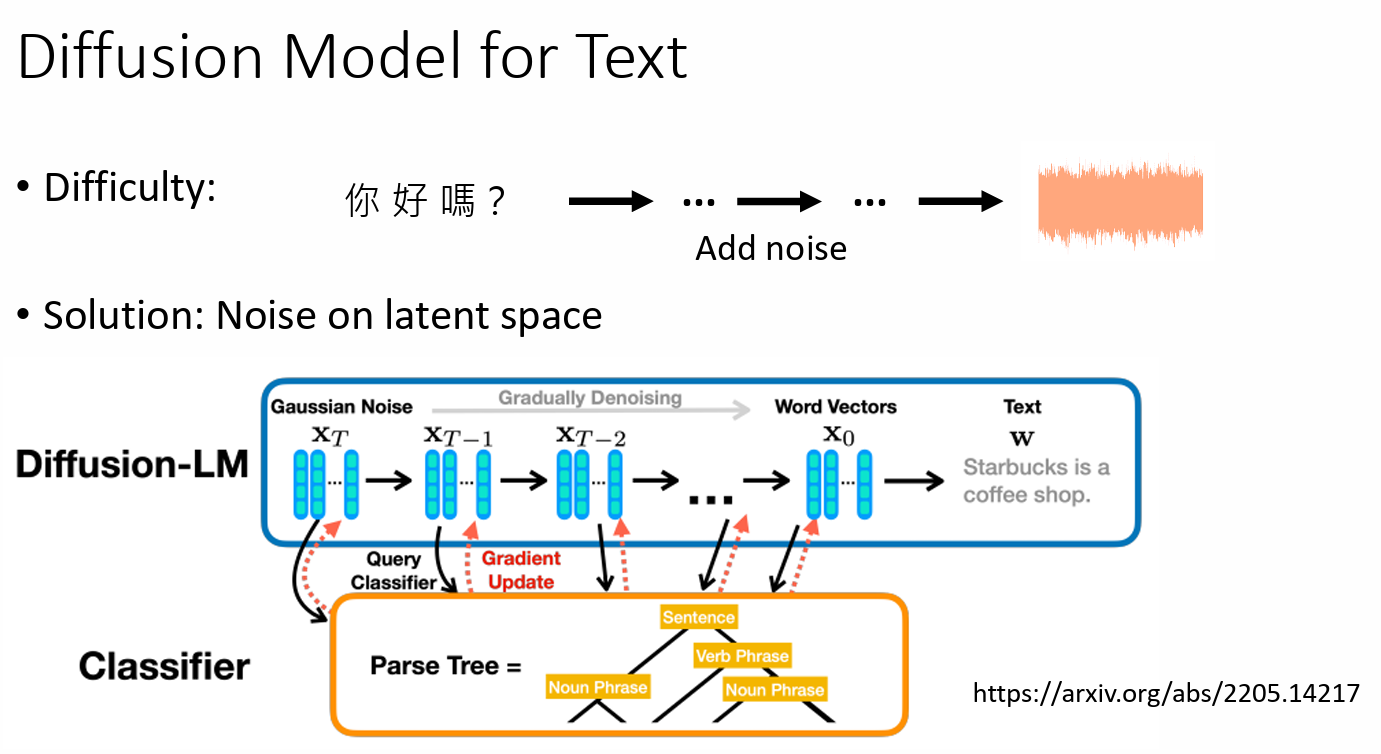
    • 不加 Gaussian noise，加其他种类的 noise
计算机视觉 图像生成
2024 - 2025 caroline's world. All Rights Reserved.
Theme Jasmine by Kent Liao
赣ICP备2024043307号 赣公网安备36060002000103号